Editions ENI Livres | Vidéos | e-Formations
Le calcul matriciel
Rappels sur les matrices
Sans rentrer dans les définitions théoriques qui sortent du cadre de cet ouvrage, nous considérons dans ce qui suit qu’une matrice se présente sous forme d’un tableau rectangulaire de n lignes et de m colonnes contenant des nombres réels. Chaque élément de la matrice peut être désigné par son index de ligne et son index de colonne :
aij représente le nombre situé à l’intersection de la ligne i et de la colonne j.
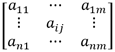
Une matrice ayant le même nombre de lignes et de colonnes est une matrice carrée.
Addition de matrices : des matrices de mêmes dimensions peuvent être additionnées. Si A et A’ sont deux matrices de dimensions n x m, l’élément générique de la matrice C = A + A’ se calcule par :
cij= aij + a’ij
Multiplication par un scalaire k : le résultat est une matrice de même dimension dont l’élément générique est :
cij= k.aij
Multiplication de deux matrices: la multiplication d’une matrice A (n lignes x m colonnes) par une matrice B (m lignes x p colonnes) est une matrice C de n lignes x p colonnes ayant pour élément générique :
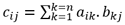
Matrice identité (I) : matrice dont tous les éléments valent 0 sauf les éléments de la diagonale qui...
Traitement des matrices dans Excel
Désignation des matrices
La forme la plus simple de désignation d’une matrice est la plage rectangulaire de cellules repérée par son adresse ou par son nom. Dans l’exemple ci-dessous, la plage A3:D6 (nommée M) représente une matrice.
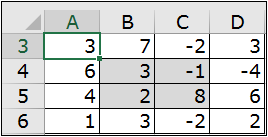
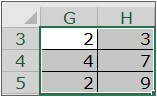
Une matrice peut également être désignée sous forme de constante matricielle. L’expression {2.3;4.7;2.9} désigne la matrice 3 lignes x 2 colonnes suivante :
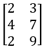
Une constante matricielle peut être utilisée sous cette forme dans une formule mettant en jeu plusieurs matrices (addition, multiplication...). Elle peut également être utilisée sous forme d’écriture "matricielle" (cf. chapitre Conseils de bonne pratique - Les formules matricielles) pour remplir une plage de cellules. Dans l’exemple la plage D11:E13 a été remplie en effectuant dans l’ordre suivant :
-
la sélection de la plage D11:E13
-
la saisie de la formule={2.3;4.7;2.9}
-
la validation sous forme matricielle par la combinaison des touches CtrlShiftEntrée.
Pour extraire une sous-matrice d’une matrice de base, il faut utiliser la fonction DECALER dont la syntaxe générale permet de désigner toute plage rectangulaire de cellules contigües à l’intérieur de cette matrice de base :
=DECALER (matrice de référence;...
Application à l’algèbre linéaire
Résolution d’un système de n équations linéaires à n inconnues
La forme générale d’un système de n équations à n inconnues est :
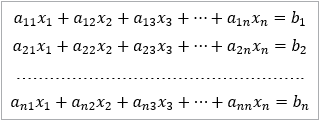
Sous forme matricielle, le système s’écrit : A.X = B, soit :
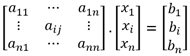
La solution s’obtient donc par la formule X = A-1.B, à condition que la matrice A soit inversible.
Exemple 1
On veut résoudre le système linéaire de 3 équations à 3 inconnues suivantes :
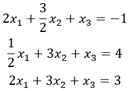
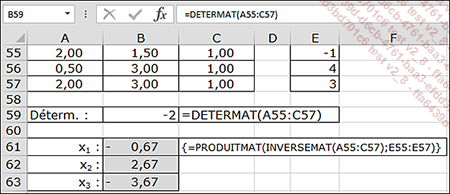
La solution du système est donnée par l’écriture matricielle :
Le déterminant étant différent de 0, la matrice est inversible.
La transcription dans Excel s’écrit comme suit :
Diagonalisation d’une matrice
La diagonalisation d’une matrice, lorsqu’elle est possible, permet de simplifier largement les calculs. Une matrice M est diagonalisable si elle peut s’écrire sous la forme : M = P-1.D.P. D est la matrice diagonale et P la matrice de passage. La matrice diagonale est constituée des valeurs propres de la matrice et la matrice P de la juxtaposition des vecteurs propres de cette même matrice.
Les valeurs propres sont les racines du polynôme obtenu par le calcul du déterminant de la matrice [λ.I - M].
Exemple
Soit la matrice :
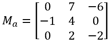
Cherchons les valeurs de x telles...
Application aux circuits électriques maillés
Les circuits électriques peuvent se présenter sous forme de mailles. La loi d’Ohm généralisée s’écrit : U + Z.I où Z est la matrice des impédances. Pour un quadripôle schématisé comme suit :
la loi d’Ohm s’écrit :
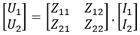
Le calcul des intensités se fait donc par inversion de la matrice des impédances. Cette matrice Z peut bien entendu être constituée d’impédances complexes. Bien qu’il n’existe pas dans Excel 2019 de fonction d’inversion de matrice complexe, il est quand même possible de résoudre le problème.
Décomposer les matrices Z et Z -1 en parties réelles et imaginaires soit : Z = A + j.B et Z -1= A’ + j.B’. Le calcul de A’ et B’ s’effectue à l’aide des relations suivantes : A’ = (A + B.A-1.B)-1 et B’ = -A-1.B.A’.
L’exemple Excel suivant est basé sur une matrice Z complexe (3x3). Les matrices A et B sont calculées grâce aux fonctions COMPLEXE.REEL et COMPLEXE.IMAGINAIRE. Ces fonctions ne fonctionnent pas en mode "matriciel". Il faut donc les utiliser sur une première cellule puis les recopier sur les 8 autres.
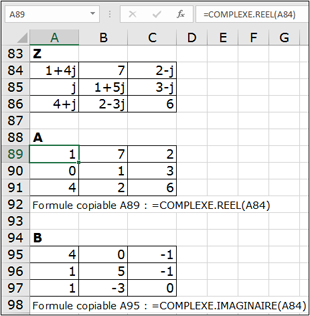
Les matrices A’et B’ sont calculées à partir des matrices A et B à l’aide...
Application des matrices aux rotations
Le calcul matriciel est très utilisé dans les applications comme le calcul des structures, l’ingénierie ou encore les jeux vidéos pour manipuler des figures géométriques et en particulier effectuer des rotations.
Les rotations planes (2D)
On considère le repère orthonormé suivant :
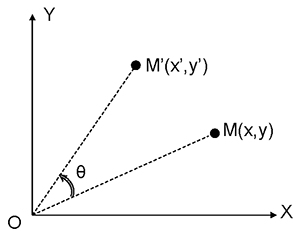
La rotation plane d’origine O et d’angle θ permet de calculer la position d’un point M’ (x’,y’) par rapport à un point origine M (x,y) par la matrice de rotation suivante :
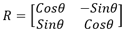
Autrement dit les coordonnées (x’,y’) du point M’ satisfont la relation matricielle :
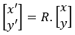
La matrice de rotation peut également s’appliquer à un polygone défini par les cordonnées de ses sommets : (x1, y1), (x2, y2), ..., (xn, yn).
On aura alors :
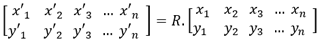
Dans l’exemple suivant une rotation de 90°(π/2) est appliquée à un rectangle dont les sommets ont pour coordonnées (1,1), (5,1), (5,2), (1,2).
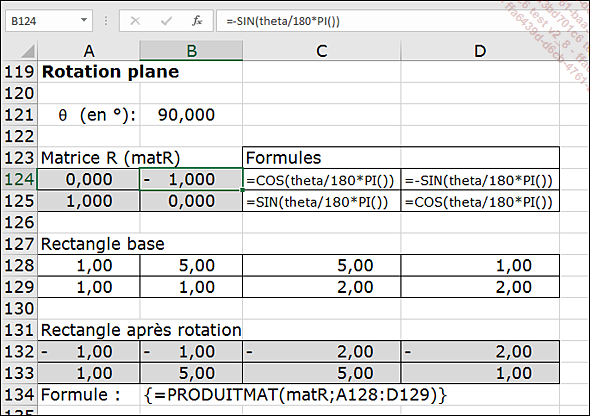
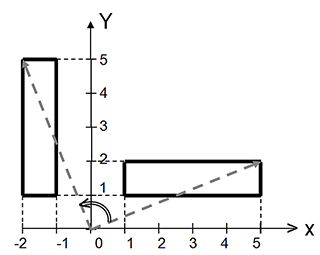
La figure suivante permet de visualiser l’opération de rotation effectuée.
Les rotations dans l’espace
Dans le cas des rotations suivant les 3 dimensions, on utilise les angles d’Euler. Ces 3 angles définissent la rotation résultant des 3 rotations élémentaires :
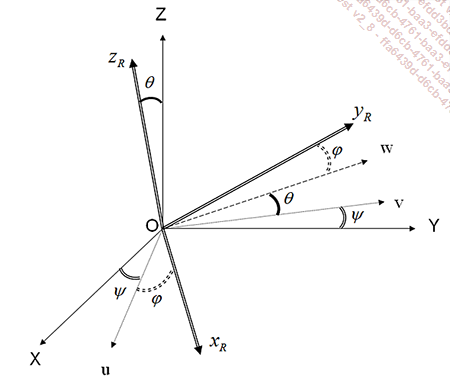
Dans la figure précédente, on passe du système d’axes...
Application des matrices en économie
La matrice des coefficients techniques
Le tableau suivant récapitule, en monnaie locale, le système des échanges entre les trois secteurs d’une économie fonctionnant totalement en autarcie.
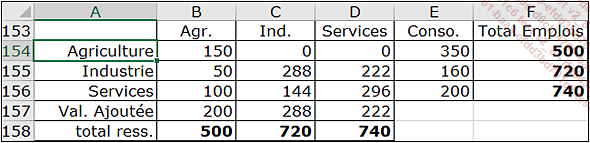
Dans ce tableau, la colonne B, qui concerne l’agriculture, indique que, pour fournir un emploi de 500 (cellule B158), les entreprises agricoles ont acheté pour 150 auprès d’autres entreprises agricoles, pour 50 à l’industrie et pour 100 auprès des entreprises de services.
La matrice des coefficients techniques est composée de nombres représentant les ressources nécessaires pour obtenir 1 unité monétaire de chaque secteur. Ainsi pour obtenir 1 unité monétaire agricole, il faut 150/500=0,3 unités agricoles, 50/500=0,1 unités d’industries et 100/500=0,2 unités de services.
La matrice des coefficients techniques, nommée MCT (plage B161:D163) se présente comme suit :
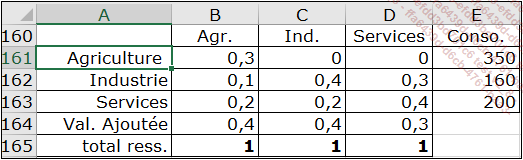
La formule de la cellule B161, recopiable dans toutes les autres cellules du tableau, est : =B154/B$158.
Nommons xA, xI, xS les ressources de chacun des secteurs pour satisfaire les consommations finales CA, CI, CS. La relation matricielle suivante est vérifiée :
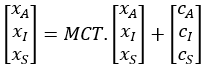ou encore 
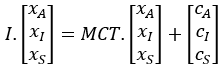, I étant
la matrice identité.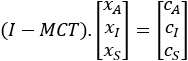
et finalement, 
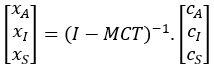.Exemple
On souhaite connaître les ressources...
