Article paru dans le magazine Programmez n°251
Le but du présent article est de rappeler succinctement les grands principes qui régissent la programmation quantique pour ensuite utiliser une des plateformes accessibles au grand public permettant d’expérimenter la programmation quantique : IBM QiSkit, utilisable complètement en ligne. Qiskit utilise le langage Python, mais peut également utiliser Swift et JavaScript. Ici nous nous contenterons de travailler avec Python en prenant l’exemple des états de Bell correspondant à ce que l’on appelle l’intrication maximale, phénomène dont nous expliquerons le fonctionnement.
Quelques notions de physique quantique
Indifféremment nommé qubit ou qu-bit, le bit quantique représente l’unité de base en informatique quantique à l’instar du bit en informatique. Ce bit quantique est associé à une particule qui se trouve être dans un certain état nommé état quantique. Cet état quantique se définit grâce à un phénomène propre à la physique quantique appelé la superposition quantique. Avant d’expliquer plus avant ce phénomène, précisons que la superposition quantique s’interrompt quand est effectuée la mesure quantique. Ainsi un bit quantique est dans un état quantique qui peut être vu comme une combinaison linéaire des différentes valeurs possibles après mesure. Cette combinaison linéaire des différentes valeurs possibles après mesure concrétise ce qu’est la superposition quantique. Une fois la mesure quantique effectuée, une seule valeur de celle qui était possible précédemment, est conservée.
Histoire de rendre tout cela plus concret, reprenons la célèbre expérience de la pensée, le chat de Schrödinger. Celui-ci va nous permettre d’illustrer chaque notion évoquée puis d’introduire une notation utilisée pour représenter un état quantique, la notation bra-ket.
L’expérience du chat de Schrödinger
Erwin Schrödinger énonce les données de son expérience ainsi.
Dans une boîte close et opaque se trouvent plusieurs éléments :
- un atome radioactif;
- une fiole de poison mortel;
- un chat.
Si l’atome se désintègre alors la fiole se retrouve ouverte, le poison se diffuse et le chat meurt instantanément. L’atome peut se désintégrer à n’importe quel moment sans qu’à l’extérieur de la boîte on puisse en avoir connaissance. Du point de vue d’un observateur extérieur, il n’y a aucun moyen de savoir si l’atome s’est désintégré et donc de savoir si le chat est mort ou vivant.
D’un point de vue quantique, on peut donc envisager le chat comme étant à la fois vivant et à la fois mort. On peut en effet établir une combinaison linéaire de l’état quantique du chat comme étant une superposition des états finaux après mesure quantique. Ici la mesure quantique est ni plus ni moins que l’ouverture de la boîte par un observateur. Une fois la boîte ouverte, le chat est soit mort soit vivant. Les deux états possibles sont en effet vivant et mort. Tant que la boîte n’est pas ouverte, l’état quantique est donc bien une combinaison des deux états superposés vivant et mort.
En notation bra-ket, on écrit un état quantique ψ du chat de la manière suivante.
Si on considère les deux états superposés du chat (vivant et mort) comme étant équiprobables alors l’état quantique du chat s’écrit comme ci-dessous :
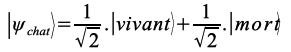
Note – le coefficient multiplicateur devant chaque état dans la précédente équation est égal à la racine carrée de la probabilité associée (ici chaque probabilité est égale à 0.5). En effet :
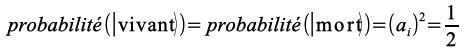
Notation bra-ket et mise en évidence de la combinatoire
Avec deux qubits, on a quatre valeurs possibles mesurables. Ce sont les valeurs suivantes :
On a en effet la combinaison linéaire suivante avec les coefficients α, β, ɣ et δ :
Comme précédemment, on peut exprimer sous forme d’équations chacune des valeurs finalement mesurables :
Si l’on passe à trois qubits, on aura huit valeurs possibles. De manière générale, une solution à n qubits verra la possibilité de travailler en 2 exposant n. On a donc accès à une combinatoire exponentielle qui permet, du moins en théorie, de résoudre des problèmes très longs à résoudre en informatique classique. Toutefois, à chaque problème, il faut ou faudrait inventer un algorithme quantique ad hoc. Ce type d’algorithme prend en entrée un ou plusieurs qubits qui seront ensuite soumis à un circuit quantique. Ce circuit quantique est composé de portes quantiques et se termine systématiquement par une mesure quantique. L’informatique classique et son algèbre de Boole manipulent des portes logiques. En informatique quantique, on utilise des portes quantiques. Les états quantiques étant finalement des états probabilistes, on soumet en général plusieurs fois les mêmes entrées à un circuit quantique. On analyse ensuite la répartition du résultat des 1000 ou 2000 mesures (une mesure par utilisation du circuit quantique).
Avant de commencer à définir et à utiliser des circuits quantiques avec IBM Qiskit, nous allons en quelques lignes expliquer une autre notion de physique quantique particulièrement utile en informatique quantique : l’intrication (ou l’enchevêtrement) quantique.
L’intrication quantique
L’intrication quantique est un phénomène physique assez étonnant dont l’existence fut longtemps controversée au sein de la communauté scientifique. Il a été depuis démontré théoriquement et reproduit à plusieurs reprises de façon expérimentale. Il consiste en la mise en évidence d’un lien entre deux particules, pourtant possiblement très éloignées l’une de l’autre. Deux particules A et B qui sont intriquées ont le même état quantique. Si l’une des deux change d’état, l’état de la seconde particule sera le même. Cela implique enfin que le résultat de la mesure respective de deux particules intriquées est le même.
Ce phénomène est fréquemment utilisé en informatique quantique pour coder ce qu’on appelle la téléportation quantique ou encore pour simuler les états de Bell, ce qui sera l’objet de notre exemple de code avec IBM Qiskit.
Les états de Bell
Un des moyens d’implémenter l’intrication de deux particules, donc de deux qubits, est de recourir aux états de Bell. Ceux-ci permettent de maximiser l’intrication entre les deux qubits. Ainsi, si on sollicite 1000 fois le circuit quantique qui permet cela, la mesure finale nous indiquera 1000 fois que les deux qubits ont la même valeur.
Un circuit quantique bien déterminé et bien connu permet d’implémenter les états de Bell. Il implique l’utilisation de deux portes quantiques, la porte de Hadamard et la porte C-NOT.
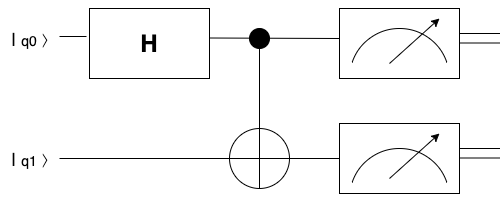
Le schéma précédent prend deux qubits en entrée (q0 et q1) soumis à une porte de Hadamard puis à une porte C-NOT pour ensuite aborder la mesure des deux sorties. En théorie, les deux valeurs mesurées doivent être identiques.
IBM QisKit
Qiskit permet de s’essayer à l’informatique quantique de plusieurs manières. En premier lieu, Qiskit s’installe et s’utilise localement indifféremment sous Linux, Windows ou macOS. L’url suivante détaille la procédure à suivre pour installer QiSkit sur votre machine : https://qiskit.org/documentation/install.html
La plateforme permet également de travailler entièrement en ligne. C’est la solution que nous utiliserons ici. D’une part, il est mis à disposition un éditeur graphique de circuits quantiques nommé Circuit Composer (nous en dirons un mot) et d’autre part, il est possible de coder et d’exécuter tous ses programmes quantiques en Python dans des notebooks Jupyter que nous allons largement utiliser ici.
Une fois défini votre circuit quantique (soit avec Circuit Composer soit au sein d’un notebook Jupyter), on peut exécuter le programme. Qiskit permet de soumettre le programme à deux types de solveurs quantiques :
- des simulateurs de machines quantiques conçus avec un ordinateur classique qui sont supposés donner un résultat exact d’un point de vue quantique ;
- de vraies machines quantiques. L’exécution se retrouve alors dans une file d’attente. En effet, ces machines quantiques sont utilisables par tous les utilisateurs IBM. Cette possibilité est susceptible de donner des résultats partiellement faux, les solveurs quantiques étant particulièrement instables.
Note – les notebooks Jupyter permettent la programmation interactive faisant alterner du code Python et le résultat graphique ou non de son exécution. L’extension d’un fichier de notebook Jupyter est .ipynb. Un tel fichier peut facilement être partagé, y compris sur des sites de gestion de développement comme Github qui savent afficher un fichier .ipynb.
Pour utiliser Qiskit en ligne, commencez par vous créer un compte IBM en ligne à l’url suivante :
https://quantum-computing.ibm.com/
Une fois votre compte créé, vous accédez à votre espace muni d’une barre latérale à gauche de l’écran qui vous permet de naviguer parmi les différents outils mis à disposition. Ci-dessous une copie d’écran de la barre latérale incluant les liens suivants.
- Dashboard, qui fait office de page d’accueil.
- Results, qui permet de consulter les exécutions passées et leurs résultats.
- Circuit Composer, qui permet de réaliser un circuit quantique de manière graphique.
- Qiskit Notebooks, qui permet de travailler avec des notebooks Jupyter.
Le Circuit Composer de Qiskit
Cet outil permet de composer son circuit quantique en faisant glisser les différentes portes quantiques de notre programme. Ainsi, en quelques clics ,on réalise le schéma suivant en faisant glisser une porte de Hadamard (H), une porte C-NOT ainsi que deux portes de mesure.
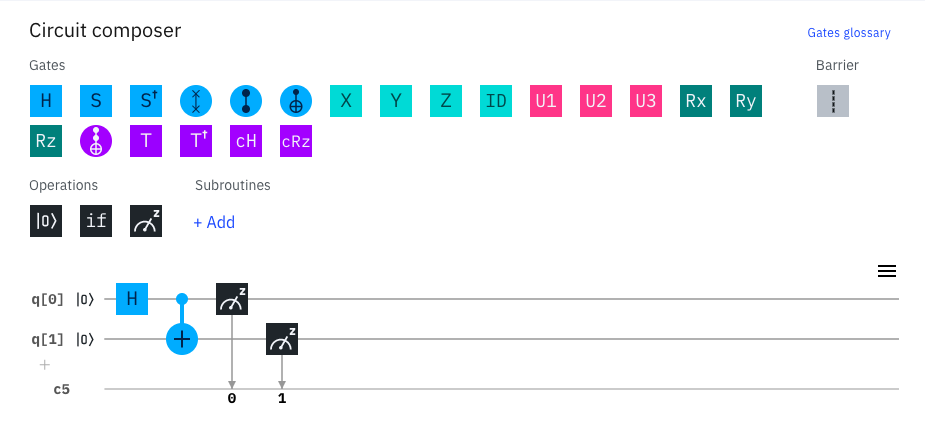
Au-dessus du schéma ainsi composé, se trouve un bouton Run dans lequel on peut sélectionner un solveur ainsi que le nombre d’utilisations du circuit quantique. Nous choisissons donc de lancer 1024 essais à l’aide d’un des simulateurs quantiques mis à disposition.
Après quelques secondes on obtient un résultat graphique qu’il s’agit d’interpréter.
Note – On n’interprète que les deux derniers digits de chaque résultat. En l’occurrence les trois premiers zéros (000) dans 00011 ne sont pas signifiants ; les deux derniers digits correspondants aux deux mesures de qubits de sortie.
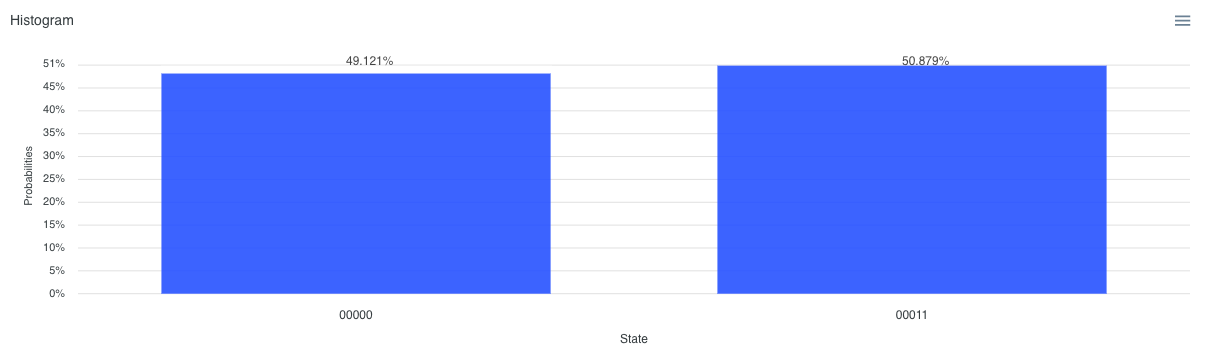
On voit qu’on obtient 49,121 % des essais (503 essais) qui donnent le résultat suivant dans lequel les deux qubits de sortie sont identiques (à zéro) :
On obtient également 50,879 % des essais (521 essais) qui donnent le résultat suivant dans lequel les deux qubits de sortie sont identiques (à un) :
C’est dans ce sens que l’on atteint un maximum d’intrication. Les deux mesures sont toujours de valeurs identiques entre elles. En effet, nous n’obtenons jamais les deux situations suivantes :
Les notebooks Jupyter dans Qiskit
Passons à présent à l’utilisation de Jupyter. Nous allons reproduire le même exemple, mais cette fois avec du code Python. Nous lancerons une simulation similaire à celle qui précède, puis nous exposerons notre programme quantique sur une vraie machine quantique située à Melbourne. Commençons à créer un nouveau notebook Jupyter en cliquant sur le bouton New Notebook.
On va ensuite à coder une première section du notebook que nous détaillons tout de suite.
On commence par écrire la clause %matplotlib inline nécessaire dès l’instant que l’on travaille avec des notebooks Jupyter.
%matplotlib inline
Puis on déclare les différents modules dont on aura besoin à commencer par Qiskit. On importe également numpy et plot_histogram pour avoir un résultat graphique.
import qiskit
from qiskit import(
IBMQ,
ClassicalRegister,
QuantumCircuit,
QuantumRegister,
QuantumCircuit,
execute,
Aer)
import numpy as np
from qiskit.visualization import plot_histogram
Puis on définit notre circuit quantique à l’aide de la fonction QuantumCircuit dont la documentation est disponible ici : https://qiskit.org/documentation/api/qiskit.circuit.QuantumCircuit.html
On a besoin de deux bits quantiques et en quelque sorte de deux bits classiques correspondant à l’emplacement de la mesure de chaque bits quantiques de sortie.
circuit = QuantumCircuit(2, 2)
Puis on adjoint une porte de Hadamard sur la première ligne de bit quantique.
circuit.h (0)
On ajoute ensuite notre porte quantique C-NOT entre la première ligne de bit quantique et la seconde ligne.
circuit.hcx (0,1)
Puis les deux unités de mesure quantique dont on interprétera les résultats.
circuit.measure ([0,1],[0,1])
Pour l’instant, on a juste défini un circuit quantique que l’on va dessiner à l’écran avant de l’exécuter.
circuit.draw()
print(circuit)
circuit.draw(output=‘mpl’, filename=‘circuit.png’)
Ci-dessous la copie d’écran de la première section de notre notebook :

Quand on l’exécute, on obtient deux représentations de notre circuit quantique :
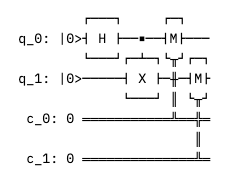
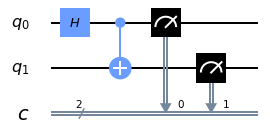
Nous allons à présent exécuter ce programme quantique. La seconde section du notebook concerne l’exécution du programme sur un simulateur quantique supposé donner un résultat parfait d’un point de vue quantique. La troisième section concerne l’exécution sur une vraie machine quantique.
Voici le code commenté de la deuxième section :
On déclare un simulateur qui sera chargé de l’exécution.
simulator = Aer.get_backend(‘qasm_simulator’)
On exécute notre circuit quantique pour 1000 essais.
job = execute(circuit, simulator, shots=(1000)
On obtient le résultat de la simulation.
result = job.result()
counts = result.get_counts(circuit)
Enfin on affiche un histogramme synthétisant les résultats.
print(“\nRésultats :”, counts)
plot_histogram(counts)
Les résultats uniquement en 00 ou en 11 confirment que l’on est bien en intrication maximale de manière parfaite (en effet, aucun artefact 01 ou 10 n’est présent même de façon minime dans les résultats).
Passons à présent à la troisième section qui utilise une vraie machine quantique.
On commence par déclarer cette machine quantique localisée à Melbourne.
provider = IBMQ.get_provider(group=(‘open’)
device = provider.get_backend(‘ibmq_16_melbourne’)
Puis on exécute notre circuit quantique sur cette machine.
job_exp = execute(circuit, device, shots=1024)
Et comme dans la deuxième section, on obtient puis on met en forme les résultats.
result_exp = job_exp.result()
counts_exp = result_exp.get_counts(circuit)
print(“\nRésultats expérimentaux:”), counts_exp)
plot_histogram(counts_exp)
Les résultats ne sont toutefois pas immédiats. Ce nouveau calcul est placé dans la file d’attente de la machine – nous ne sommes pas les seuls à la solliciter. On peut voir, peu après son lancement, son état et sa présence dans la file d’attente dans l’onglet Results.

Ci-dessous la copie d’écran de la troisième section de notre notebook ainsi que son résultat obtenu après quelques minutes :
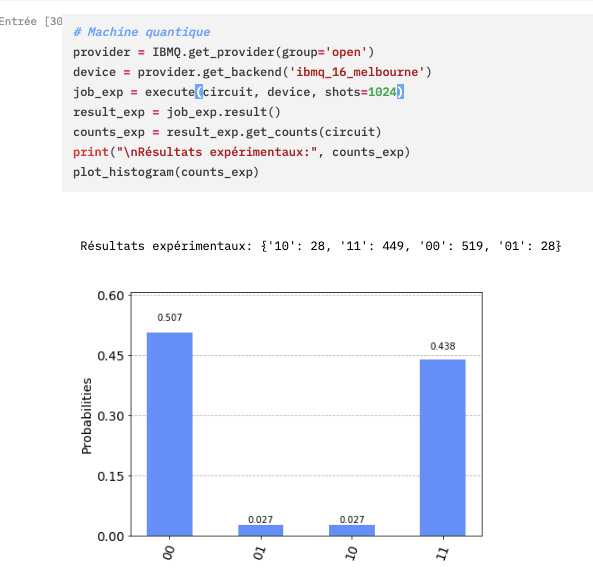
On voit donc que la machine quantique fonctionne plutôt bien, mais qu’elle a quelques défauts et approximations. Ainsi, un peu moins de 6% des tirages ont conduit à obtenir 01 ou 10 ce qui est en contradiction avec le principe même de l’intrication maximale. Le simulateur quantique utilisé précédemment ne produisait pas de tels artefacts. Certes, cette exécution montre un défaut (faible) mais elle a été lancée sur une vraie machine quantique, ce qui est tout à fait exaltant.
À vous de jouer à présent 🙂
Benoît Prieur est développeur indépendant pour sa société Soarthec. Il est par ailleurs l’auteur du livre d’introduction à l’informatique quantique De la physique quantique à la programmation quantique en Q# publié aux éditions ENI en février 2019. Il a également assuré en fin d’année 2019 des cours d’informatique quantique auprès d’élèves ingénieurs de l’ECE Paris.


