Par Ludivine Crépin, doctoresse en intelligence artificielle et auteur aux Editions ENI

Grâce à l’évolution constante et exponentielle des performances des ordinateurs, les réseaux de neurones sont disponibles pour tous avec notamment des frameworks comme Tensorflow, Pytorch ou encore Scikit. Développer un outil de Machine Learning semble assez simple aujourd’hui mais vous rendez-vous compte de la complexité qui se cache derrière ses outils ?

Eh oui, si nous regardons leurs entrailles, nous sommes en plein dans l’algorithmie et la théorie des graphes ! Je vous propose d’explorer comment sont construits ces réseaux de neurones en commençant par leur origine.

Un peu d’histoire

 C’est en 1943 que le premier réseau de neurones est modélisé dans les travaux de McCulloch et Pitts, alors que le terme « Intelligence Artificielle » (1956 environ) n’existait pas, ainsi que celui de « Machine Learning » (1959). Les ancêtres de nos ordinateurs non plus d’ailleurs…

Notons que la plupart des modélisations des grands principes de l’IA ont été inventés dans la seconde partie du XXème, bien avant l’ordinateur.

 Si la modélisation existe depuis 1943, pourquoi n’avons-nous pas exploité les réseaux de neurones et le machine learning bien avant les années 2010 ? Tout simplement car les ordinateurs ne pouvaient pas assumer l’exécution d’un tel programme. Ce sont d’ailleurs ces réseaux qui ont sorti l’IA qui hibernait dans son hiver blanc depuis les années 1990.

Au vu de la complexité algorithmique des réseaux de neurones, ils demandent pour leur apprentissage des ressources assez importantes en termes de calculs et de mémoire : mémoire vive pour supporter l’exécution et mémoire disque pour stocker les données d’apprentissage qui dépassent régulièrement les dizaines de giga.

Du neurone humain au perceptron

Les réseaux de neurones s’inspirent des neurones animaux. Un neurone naturel peut être vulgarisé comme une cellule qui s’active ou non en fonction de l’intensité électrique qu’elle reçoit, un interrupteur en somme.

Le neurone artificiel, le perceptron, est également un interrupteur : selon son entrée, il active ou non sa sortie. En informatique, nous ne pouvons pas faire varier l’intensité du courant, le courant passe (1) ou ne passe pas (0). Nous devons donc utiliser une fonction d’activation pour savoir si le perceptron est activé selon son entrée booléenne.

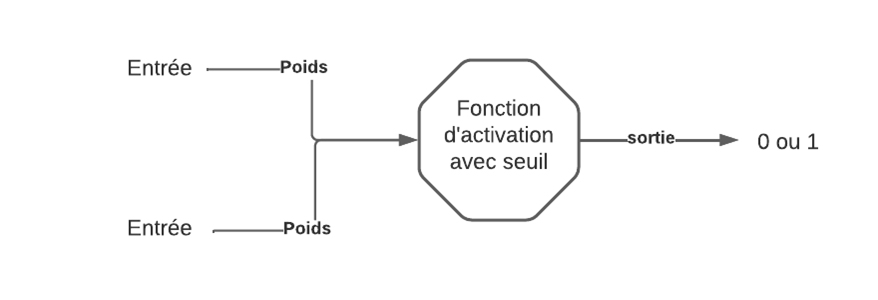
Pour illustrer le fonctionnement d’un perceptron, prenons une fonction d’activation simple : un seuil avec la fonction « heaviside » (il en existe bien d’autres mais trop complexes pour un calcul mental).

Un perceptron a une et une seule sortie. Chaque entrée du perceptron peut avoir deux valeurs : 0 ou 1. Pour correctement configurer notre perceptron, nous ajoutons des poids à ces entrées compris entre [-1 ;1]. Pour activer le perceptron, c’est-à-dire obtenir 1 en sortie, il faut que la somme pondérée des entrées soit supérieure ou égale au seuil fixé.

Pour qu’un perceptron puisse apprendre, nous devons lui fournir des données dont nous connaissons la sortie. Son apprentissage réside en la détermination de la valeur des poids des entrées, le seuil étant fixé.

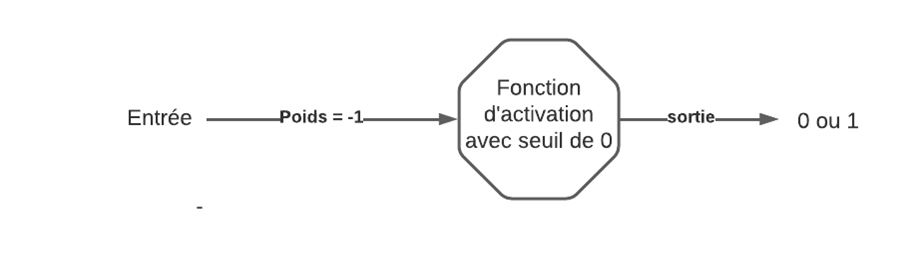
Prenons l’exemple le plus simple : le NON logique. Cet opérateur est unaire donc nous aurons une seule entrée. Si cette entrée est activée, la sortie doit être inactive et vice versa. Fixons notre seuil à 0. Nous devons trouver un multiplicateur de 1 qui nous donne un chiffre négatif. Nous choisissons donc -1 et cela nous arrange bien car pour l’entrée à 0, nous avons une somme pondérée nulle donc la sortie du perceptron est activée. Nous avons donc un perceptron qui a appris le NON logique.

Du perceptron au réseau de neurone

Un perceptron peut apprendre les opérateurs logiques de base mais dès que nous arrivons au stade du « OU exclusif », il ne suffit plus, il faut lier plusieurs perceptrons pour son apprentissage, donc utiliser un perceptron multicouche, i.e. un réseau de neurone.

La couche d’entrée d’un réseau de neurones est constituée d’autant de neurones que d’entrées possibles. Par exemple, dans le cas de l’apprentissage de chiffres digitaux, il nous faut 7 entrées, un neurone pour chaque barre possible.

La couche de sortie contient autant de neurones que de possibilités. Pour la reconnaissance des chiffres digitaux, il y aura donc naïvement 10 sorties possibles, une par chiffre. Nous pouvons également les réduire à quatre neurones pour représenter les chiffres en binaire en sortie.

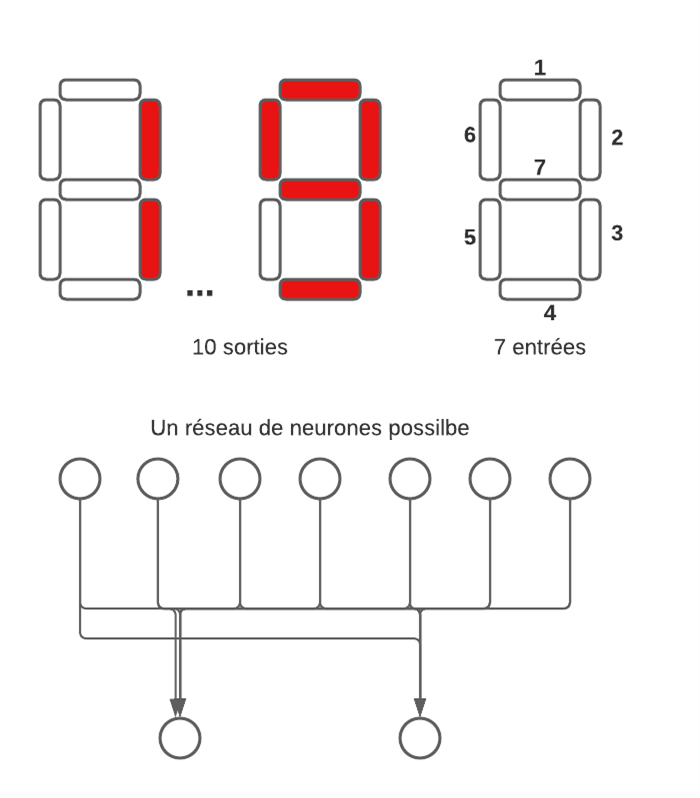
Nous remarquons que la structure utilisée pour le réseau de neurone est bien un graphe orienté. Les neurones sont les sommets de ce graphe et les connexions entre eux les arrêtes. Implémenter un graphe quelconque relève d’une difficulté largement plus grande qu’implémenter une liste ou un arbre. En effet, il n’y a aucune règle sur les connexions des sommets, n’importe quel sommet peut être connecté à un autre.

Maintenant nous allons modéliser un réseau pour classifier des images avec l’exemple pédagogique, donc simple, fashion minst.

Les images ont 28 pixels de hauteur et de largeur, ce qui nous fait donc 784 neurones d’entrées. Les données permettent de trier les images en 10 classes, donc 10 neurones en sortie. Passer directement de 900 neurones à 10 est un peu abrupt et très compliqué pour trouver les bons poids…

En effet, pour déterminer les poids de chaque neurone, le réseau va parcourir chaque donnée d’entrainement, les unes après les autres, et ce tant que les poids des neurones ne sont pas bien calibrés.

Le calcul de l’erreur revient à faire une estimation de la déviation des poids pour obtenir les sorties attendues. Sa diffusion au sein du réseau est appelée la rétropropagation du gradient qui oblige un parcours du graphe en sens inverse de son orientation de base, l’information devant être diffusée des sorties vers les entrées et non plus en sens inverse.

Ici je ne fais que vulgariser les structures de données et les algorithmes implémentés. Juste avec ces éléments, vous devez commencer à entrevoir la complexité des réseaux de neurones !

Revenons à nos images. Il nous faut donc utiliser des couches cachées dans notre réseau, sans quoi nous avons beaucoup de chance que notre réseau n’arrive jamais à trouver un bon gradient.

Il n’existe pas vraiment de lois mathématiques pour déterminer le nombre de couches cachées, ni leur nombre de neurone. Il faut faire en sorte de représenter un entonnoir entre la couche d’entrée et la couche de sortie.

Avec un réseau assez simple en connexions locales, nous avons besoin de deux couches cachées : la première de 300 neurones ayant 784 entrées chacun et la deuxième de 100 neurones ayant 300 entrées chacun. Et finalement une couche de sortie avec 10 neurones possédant donc 100 entrées chaque. Soit un graphe de 1194 sommets et 30 235 200 arrêtes juste pour apprendre des petites images pixélisées…

Dès que nous dépassons le réseau de neurones en connexions locales avec les réseaux récurrents (RNN) ou encore les convolutifs (CNN), nous ne sommes plus sur un graphe simple mais sur un graphe complexe qui contient des boucles, les connexions entre les neurones n’étant plus seulement entre deux couches. Cela complexifie encore plus l’implémentation, les calculs et la rétropropagation de l’erreur. Je vous laisse imaginer la complexité d’un tel code…

Il nous faut applaudir les développeurs de ces frameworks qui arrivent à générer de tels graphes de manière totalement générique avec différents types de réseau, différentes fonctions d’activation, différentes types de couches, différentes métriques et j’en passe. Chapeau bas !

Cependant seront-ils encore capables de développer avec une telle qualité les réseaux de demain ?

Et demain ?

Nous entrevoyons donc la complexité algorithmique des réseaux de neurones pour leur apprentissage, sans parler des soucis de mémoire disque pour les données d’apprentissage. Comme il y a un décalage entre la modélisation et l’implémentation des réseaux de neurones, il en va de même pour les futures évolutions du Machine Learning. Une modélisation conçue début 2000 commence à être implémentée : les réseaux de neurones liquides. Ce type de réseau demande moins de neurones, donc moins de calculs, et sera peut-être le futur du Machine Learning. Leur point fort repose sur des équations différentielles qui peuvent être modifiées en temps réel après l’apprentissage. Tout en gardant les neurones connectés, ces réseaux sont également moins rigides sur ces connexions car elles sont aléatoires. L’algorithmie et le théorie des graphes seront toujours au cœur des réseaux de demain, un réseau étant forcément un graphe !

Si vous voulez en savoir plus sur le sujet, consultez le dernier livre de Ludivine Crépin,