Passons en mode confirmé
Les pointeurs et références
1. Implémentation de la mémoire
Lorsque nous exécutons un programme sur un ordinateur, ce dernier doit stocker toutes les informations de ce programme pour le faire tourner correctement. Pour stocker les données en cours d’exécution, il utilise une zone mémoire qui lui est dédiée, sa pile (ou stack en anglais).
La pile fonctionne comme une pile d’objets dans la vraie vie : nous pouvons récupérer un objet de la pile en commençant par l’objet du dessus, donc le dernier à être mis dans la pile. Le premier objet de la pile est donc le dernier que nous pouvons récupérer.
La pile ne peut pas se souvenir d’un élément précis vu qu’ils sont dépilés, donc sortis de la pile, au fur et à mesure de l’exécution du programme. Ce système permet à la pile d’être extrêmement rapide pour exécuter les instructions car justement elle ne retient rien.
Nous pouvons voir cette pile comme un espace compact où chaque case possède une taille fixe en octets et surtout avec un nombre de cases fixe pour simplifier son implémentation.

Pile utilisée lors de l’exécution d’un programme
Prenons un exemple vulgarisé avec notre structure de données représentant...
Les listes chaînées
Les tableaux ont comme limite leur taille fixe : soit nous connaissons en avance les dimensions exactes du tableau et nous sommes certains qu’elles ne changeront jamais, soit, dans le doute, nous lui attribuons des dimensions plus grandes que nécessaire pour anticiper les modifications futures, quitte à perdre de l’espace mémoire (les cases non utilisées du tableau).
Pour pallier le problème de la taille fixe des tableaux, il existe des structures complexes de données, comme les listes. Les listes ont une allocation mémoire dynamique : leur taille augmente à la demande du développeur.
Une liste est un ensemble de "maillons", liés entre eux par un pointeur et contenant une valeur, équivalente à la case d’un tableau à une dimension.
La plupart des langages de programmation implémentant ces structures complexes, le lecteur a tout avantage à en connaître le fonctionnement afin de mieux comprendre ce qui est codé au sein du langage, donc de mieux programmer et de programmer de manière plus efficiente.
1. Listes simplement chaînées
Les premières listes sont les listes simplement chaînées. Ce type de liste ne peut être lu qu’à partir du premier maillon jusqu’au dernier.
Contrairement aux tableaux, quel que soit le type de la liste, l’opérateur d’indexation [] n’existe pas. L’accès à une liste est uniquement séquentiel : chaque maillon permet d’aller au suivant, toujours en commençant par le premier.
a. Création
Pour créer une liste simplement chaînée, nous devons d’abord représenter ce qu’est un maillon. Pour ce faire, nous allons utiliser une STRUCTURE contenant deux champs, représentée dans la figure ci-dessous :
-
La valeur de la donnée.
-
Le pointeur vers le maillon suivant.

Représentation d’une liste simplement chaînée
Pour indiquer que le maillon est le dernier de la liste, le champ suivant pointera sur la valeur NULL.
STRUCTURE maillon
DEBUT
valeur : type
*suivant <- NULL : maillon
FINSTRUCTURE Tout comme les tableaux, les listes ne peuvent contenir que des valeurs de même...
Les arbres
1. Principe
Un arbre en algorithmie est réellement inspiré des arbres de la nature. Ce sont des structures composées d’une racine, le point d’accès, ainsi que de branches et de feuilles, les points intermédiaires et terminaux. Nous ne pouvons parcourir un arbre qu’en partant de la racine. Chaque branche peut être vue comme un sous-arbre, comme illustré dans la figure ci-dessous, avec sa racine et ses branches. Cette définition nous inspire fortement une structure utilisant la récursivité.
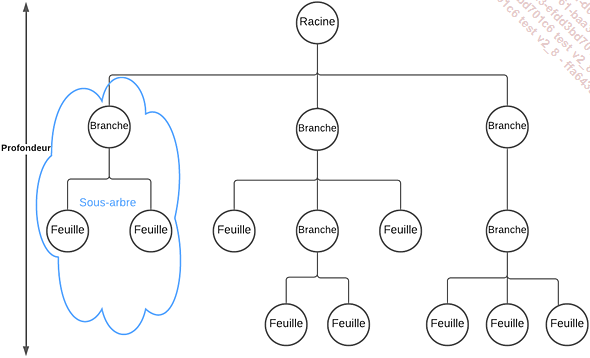
Arbre quelconque
Nous utilisons, nous aussi, des arbres dans notre vie. L’exemple le plus flagrant pour illustrer cette structure complexe est l’arbre généalogique.
2. Création
L’arbre est créé grâce à une structure complexe de données qui, comme la liste, va se construire sur une autre STRUCTURE : les nœuds. Un nœud d’un arbre peut être la racine, une branche ou une feuille. Chaque nœud va donc posséder une liste d’autres nœuds, sauf les feuilles par lesquelles cette liste sera une liste vide.
Un arbre vide est donc une STRUCTURE contenant un pointeur sur un nœud initialisé à NULL.
Chaque arbre possède également une caractéristique décrivant son nombre de niveaux : la profondeur. Nous pouvons vulgariser la profondeur par le nombre de fois où nous pouvons descendre dans l’arbre. Par exemple, l’arbre de la figure précédente a une profondeur de trois. Un arbre ne contenant qu’une racine aura une profondeur de zéro.
Dans cette section, nous nous focalisons uniquement sur les principes des arbres et leurs manipulations du fait de la possibilité qu’un nœud puisse avoir un nombre maximum illimité de nœuds sous lui. La partie algorithmique sera vue dans la section suivante sur un type d’arbre précis, les arbres binaires, pour des raisons pédagogiques.
Étudions maintenant les différents parcours des arbres.
3. Parcours en largeur
Le parcours en largeur d’un arbre consiste à parcourir l’arbre par niveau. Nous commençons par la racine puis par les branches de la racine, puis les branches des branches et ainsi de suite jusqu’aux feuilles.
Le parcours en largeur...
Et avec Python ?
En ce qui concerne les listes, Python n’implémente pas les tableaux à taille fixe, il implémente directement ces structures complexes grâce au type de données list qui possède une allocation dynamique de la mémoire. La gestion des pointeurs est entièrement effectuée par le langage, ce qui simplifie largement les programmes.
Cependant, Python ne possède pas de type de données correspondant aux arbres par défaut.
Nous vous proposons d’implémenter ces types de données complexes dans le dernier chapitre de cet ouvrage grâce à la notion d’objet car Python ne possède pas le type STRUCTURE, ce langage utilise l’objet pour nous permettre de créer nos propres types de données complexes.
Exercices
1. Exercice 1
Avec les structures et procédures de ce chapitre, créez un sous-programme pour rechercher une valeur dans une liste simplement chaînée.
2. Exercice 2
Avec les structures et procédures de ce chapitre, créez un sous-programme pour rechercher une valeur dans une liste doublement chaînée.
3. Exercice 3
Avec les structures et procédures de ce chapitre, créez un sous-programme pour rechercher une valeur dans un arbre binaire.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

