Les modèles linéaires généralisés

Modèles linéaires classiques

1. Rappel

Un modèle linéaire (cf. chapitre La régression) n’est pas nécessairement un modèle basé sur une équation linéaire telle que , mais il est toujours basé sur une fonction de lien qui unit la variable réponse à la ou aux variables explicatives. Le choix entre les modèles linéaires simples et multiples (cf. chapitre La régression) et l’ANOVA (cf. chapitre La comparaison de deux groupes) et les autres dépend des variables explicatives (cf. figure 07-01). En effet, l’ANOVA est réalisée lorsque les variables explicatives sont qualitatives et la régression sur des variables réponses quantitatives.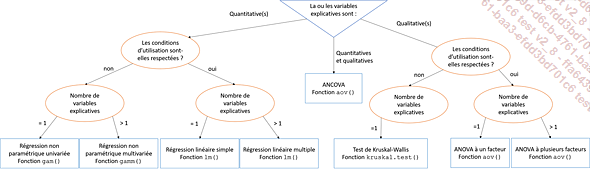

Figure 07-01 : Choix entre régression linéaire simple, régression linéaire multiple, ANOVA et autres. Dans tous les cas pris en compte ici, la variable réponse est quantitative et suit une loi normale.

La fonction aov() du package {stats} qui permet de faire des ANOVA ou des ANCOVA dans R permet aussi de réaliser des régressions linéaires, et la fonction lm() du package {stats} permet quant à elle de réaliser des ANOVA ou ANCOVA. En effet, le modèle à ajuster est de la forme pour les modèles linéaires et les analyses de la variance.

lm(Petal.Length ~ Sepal.Length, data = iris) %>% anova() 
aov(Petal.Length ~ Sepal.Length, data = iris) %>% anova() 
 
lm(Petal.Length ~ Species, data = iris) %>% anova() 
aov(Petal.Length ~ Species, data = iris) %>% anova()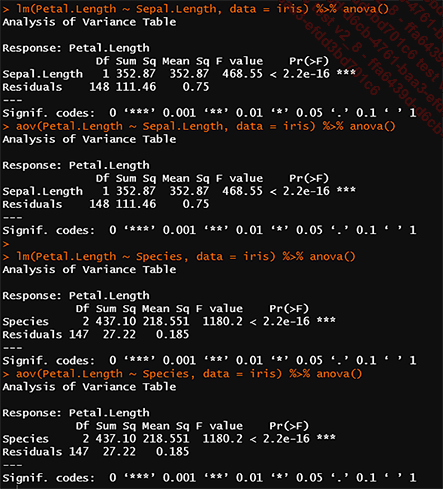 

Figure 07-02 : La régression linéaire simple ou la régression linéaire multiple et l’ANOVA à un ou plusieurs facteurs sont identiques car elles reviennent à résoudre une équation linéaire.

Tous les modèles...

Généralisation des modèles linéaires en R

1. Utilisation des modèles linéaires généralisés

Les modèles linéaires généralisés, ou GLM (Generalised Linear Models) ont trois caractéristiques :

• La fonction de lien. Elle lie la variable réponse au prédicteur, c’est-à-dire la partie réponse de l’équation, et à l’erreur f. La nature du lien donne son nom au GLM utilisé.

Distribution	Type de données	Type de GLM	Fonction de lien
Normale gaussienne	Variable quantitative suivant une loi normale	Modèle linéaire classique	f(y) = y identity()
Poisson	Comptage	Régression de poisson Modèle log-linéaire	f(y) = (y) log()
Binomiale	Variable binaire (qualitative à deux modalités)	Régression logistique Modèle logit linéaire	logit()
Gamma	Durée	Modèle gamma linéaire avec fonction inverse	inverse()

• Un prédicteur linéaire. Ce terme compliqué se rapporte à la partie réponse de l’équation. Comme pour les modèles linéaires classiques déjà vus, la partie explicative est composée de l’addition des variables prédictives : . C’est la raison pour laquelle on parle de modèles linéaires.
• Une erreur. La forme de l’erreur est dépendante de la fonction de lien. Par exemple, les erreurs d’un modèle linéaire classique suivent une loi normale, alors que celles de la régression de Poisson suivent une loi de Poisson.

L’équation s’écrit .

Les modèles linéaires généralisés lient une variable réponse à une ou plusieurs variables explicatives. Si la variable réponse est quantitative et si les données...

Modèles linéaires mixtes

Traitement des données manquantes dans les GLM

Il arrive que le jeu de données ne soit pas complet, c’est-à-dire que certaines variables ne soient pas disponibles une ou plusieurs fois. L’absence de données peut être due à un défaut dans le plan d’expérience, à une mesure perdue ou non prise, à une personne qui refuse de répondre ou à un défaut d’enregistrement, à l’appareil de mesure qui a un raté…

Ce problème assez courant doit être traité en deux étapes : une étape de détection (cf. section Détection et visualisation des données manquantes dans R, chapitre Les statistiques) et une étape de traitement.

Pour les fonctions lm(), glm() du package {stats}, lmer du package {lme4} et lme() du package {nlme}, le traitement automatique des données revient à supprimer les lignes concernées. Cette solution radicale est rarement une bonne idée. En effet, pour la personne qui fournit les données, les voir ainsi supprimées n’est jamais agréable et surtout est associé à un coût non négligeable. Avec ces fonctions, le traitement des données manquantes doit donc se faire en amont, ce qui n’est pas le cas avec les fonctions utilisées dans le chapitre L’analyse en composantes principales.

La question principale à se poser est de savoir ce que signifient les valeurs manquantes.

Petit déroulé de la démarche à adopter face aux valeurs manquantes :

Modèles non linéaires à effets fixes ou mixtes

Les modèles linéaires généralisés acceptent différentes fonctions de lien. Il est possible de ne pas en utiliser lorsque le lien entre la variable réponse et les variables explicatives n’a pas de forme prédéfinie. Ce type d’étude est très contraignant, car elle nécessite au préalable de déterminer la fonction mathématique qui explique le nuage de points.

Il existe différents packages qui peuvent convenir à beaucoup de situations. Il faut commencer par faire une recherche en s’appuyant sur les analyses passées et publiées pour déterminer le type de modèles à utiliser ainsi que les paramètres initiaux à fournir. En effet, contrairement aux modèles linéaires généralisés, les modèles non linéaires partent de paramètres initiaux fournis par l’utilisateur et les affinent. Ainsi, il est possible que cela ne converge pas.

Ce type d’étude demande un niveau plus poussé en statistiques et en connaissances des données et ne sera pas abordé dans cet ouvrage. Du coup, il arrive que dans certains cas, les modèles linéaires ne conviennent pas ou qu’il n’y ait pas de variable réponse définie ou à étudier. Dans ce cas, comment traiter les données ? Comment comprendre quelles sont les données qui interagissent ? L’objectif de l’analyse en composantes principales (cf. chapitre L’analyse en composantes principales) est précisément de déterminer dans un grand jeu de données quelles sont les variables qui le définissent au mieux. Une autre approche similaire, non développée dans ce livre...