Les procédures et fonctions
Présentation
Les algorithmes réalisés avant ce chapitre utilisent ce qui se nomme le paradigme de programmation impérative. Un paradigme de programmation est une façon de programmer et il propose un certain nombre d’outils le permettant. Le paradigme de programmation impérative donne des ordres au travers des instructions qui se succèdent et propose différentes structures de contrôle permettant de sauter ou de refaire certaines parties en fonction de conditions.
Nous pouvons constater que cette manière de procéder a quelques limites. Les algorithmes deviennent de plus en plus longs au fur et à mesure que leur complexité augmente et il est de plus en plus difficile de s’y retrouver. De plus, il peut y avoir du code qui est dupliqué, car il est nécessaire de l’exécuter plusieurs fois à différents endroits de notre algorithme.
Dans ce chapitre, nous allons découvrir un deuxième paradigme de programmation. Il se nomme le paradigme de programmation procédurale. Il ne vient pas remplacer le précédent, mais il le complète.
Afin de pallier les limitations précédemment citées, le paradigme de programmation procédurale introduit une nouvelle notion : il s’agit des sous-algorithmes. Un algorithme peut faire appel à un sous-algorithme pour réaliser...
La déclaration d’un sous-algorithme
La déclaration d’un sous-algorithme est très similaire à celle d’un algorithme.
1. Déclaration d’une procédure
Afin de déclarer une procédure, il faut utiliser la syntaxe suivante :
Procédure nomDeLaProcédure(listeDesParamètres)
#Déclarations
Début
#Instructions
Fin Pour une procédure, seule la première ligne change. Tout d’abord, le mot-clé Algo est remplacé par le mot-clé Procédure. Ensuite, après le nom de la procédure, il y a un couple de parenthèses dans lesquelles il est possible de passer des paramètres. Les paramètres sont les informations nécessaires à la procédure pour qu’elle puisse réaliser sa tâche. La procédure écrire() prend par exemple en paramètre le texte à afficher sur la console. La liste de paramètres est une suite de couples nom : type séparés par des virgules. Les paramètres sont comme des variables qui sont initialisées lors de l’appel de la procédure.
Cette première ligne s’appelle la signature de la procédure.
Exemple de déclaration d’une procédure :
Procédure afficheNfois(t : texte, n : entier)
Variable i : entier
Début
Pour i <- 1 à n
écrire(t)
FPour
Fin Dans cet exemple, la procédure prend en paramètres deux valeurs : d’une part t, de type texte, le message à afficher, et d’autre part n, de type entier, le nombre...
L’appel à un sous-algorithme
1. L’appel à une procédure
Pour faire appel à une procédure, il faut simplement écrire le nom de la procédure suivie, entre parenthèses, des valeurs permettant d’initialiser les paramètres dans l’ordre dans lequel ceux-ci sont attendus.
Exemple :
Algo Punition
# demande à l'utilisateur le texte à copier et le nombre de fois
# qu'il faut le copier
Variable phrase : texte
Variable nbFois : entier
Début
phrase <- saisir("Quelle phrase avez-vous à copier comme punition ?")
nbFois <- saisir("Combien de fois avez-vous eu à la copier ?")
afficheNfois(phrase, nbFois)
Fin L’appel à la fonction afficheNfois() est réalisé en passant en paramètre la valeur de la variable phrase et la valeur de la variable nbFois. L’ordre est très important : la première valeur passée en paramètre est recopiée pour initialiser le premier paramètre, c’est-à-dire le paramètre t, et la seconde valeur est recopiée dans le paramètre n. Si jamais l’ordre est inversé, cela ne fonctionne pas, car les types ne sont pas compatibles.
Pour les valeurs passées en paramètres, il est possible d’utiliser des variables, comme...
La transmission d’informations entre un sous-algorithme et l’algorithme appelant
L’algorithme principal possède ses variables et ses constantes, et les sous-algorithmes possèdent également leurs propres variables et leurs propres constantes. Les uns ne peuvent pas accéder aux variables des autres et inversement. Ainsi, chaque algorithme et sous-algorithme est responsable de ses variables et il ne craint pas qu’un autre sous-algorithme vienne, sans qu’il soit au courant, modifier les valeurs de ses variables. Pour les constantes, il est possible de les déclarer à un niveau global, sans risque pour autant, puisqu’une constante n’est pas modifiable.
La séparation des variables les sécurise, ce qui est très bien, néanmoins il est nécessaire de pouvoir échanger des informations entre un algorithme et le sous-algorithme auquel il fait appel. C’est grâce au mécanisme des paramètres que des valeurs peuvent être transmises au sous-algorithme. Pour transmettre une valeur depuis le sous-algorithme vers l’algorithme l’ayant appelé, c’est la valeur retournée par la fonction qui doit être utilisée.
Voici le principe illustré sur l’exemple de la fonction puissance() :
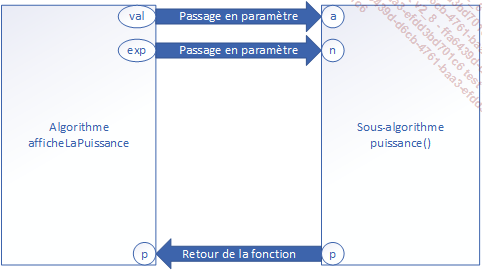
À la fin d’un sous-algorithme, toutes les variables qu’il possédait et les paramètres sont détruits.
1. Les constantes globales
Les constantes globales sont accessibles depuis n’importe quel algorithme ou sous-algorithme. Pour indiquer cela, elles sont déclarées au même niveau que celui où sont déclarés l’algorithme et ses sous-algorithmes.
Exemple :
Constante GLOBALE : entier <- 42
Algo TestConstantes
Constante LOCAL : entier <- -77
Début
écrire("il est possible d'accéder à la constante GLOBALE : " & GLOBALE &
...La récursivité
Il est tout à fait possible qu’un sous-algorithme s’appelle lui-même. C’est ce qui se nomme un appel récursif. Cela peut paraître surprenant, mais dans certaines situations, cela permet de simplifier grandement le code à écrire.
Reprenons notre premier exemple de procédure. afficheNfois() peut être transformé en une version récursive de la manière suivante :
Algo PunitionRecursive
# demande à l'utilisateur le texte à copier et le nombre de fois
# qu'il faut le copier
Variable phrase : texte
Variable nbFois : entier
Début
phrase <- saisir("Quelle phrase avez-vous à copier comme punition ?")
nbFois <- saisir("Combien de fois avez-vous eu à la copier ?")
afficheNfoisRec(phrase, nbFois)
Fin
Procédure afficheNfoisRec(t : texte, n : entier)
Début
écrire(t)
Si n - 1 > 0 Alors
afficheNfoisRec(t, n-1)
FSi
Fin La procédure afficheNfoisRec() est bien récursive puisque parmi ses instructions, elle s’appelle elle-même. L’idée de cette procédure est de dire que pour afficher n fois un message, il faut l’afficher une fois, puis qu’il reste encore à l’afficher n-1 fois. Et pour cela, il faut refaire le même traitement, donc appeler la même procédure pour afficher n-1 fois le message.
Dans l’algorithme principal, cette procédure est appelée une première fois avec en paramètres la phrase à afficher et le nombre de fois qu’elle doit l’être. Supposons que cette valeur saisie par l’utilisateur vaille 3. La procédure afficheNfoisRec() commence donc par s’exécuter une première fois. Elle affiche une première fois le message. Ensuite, la condition est testée : n valant 3, elle est vraie. La procédure afficheNfoisRec() est donc appelée une deuxième fois. Le message est donc affiché une deuxième fois. À nouveau, la condition est testée, et comme n vaut...
Exercices
1. C’est le plus grand
Écrire une fonction prenant deux valeurs réelles en paramètres et qui retourne la plus grande des deux.
Écrire une autre fonction prenant également deux valeurs réelles en paramètres, mais qui retourne :
-
0 si les deux valeurs sont égales ;
-
1 si c’est la première valeur qui est la plus grande ;
-
-1 sinon.
Écrire un algorithme principal faisant appel à ces deux fonctions.
2. Micro bataille navale (version 2)
Prérequis : Exercice 8 du chapitre Les tableaux
Reprendre l’algorithme de la bataille navale en le découpant en procédures et fonctions :
-
Écrire une procédure initialiserPlateau() qui initialise le plateau de jeu.
-
Écrire une procédure afficherPlateau() qui, comme son nom l’indique, affiche le plateau de jeu.
-
Écrire une fonction saisirEntierEntreBornes() qui fait saisir à l’utilisateur une valeur jusqu’à ce que celle-ci soit comprise entre une valeur minimum et une valeur maximum passées en paramètres de cette fonction.
-
Écrire une fonction tirer() qui permet au joueur de choisir ses coordonnées de tir et retourne vrai si le bateau est touché et faux sinon.
-
Écrire l’algorithme principal faisant appel à ces procédures et ces fonctions.
3. Un tableau et des fonctions
Écrire...
Solutions des exercices
1. C’est le plus grand
Fonction max(a : réel, b : réel) Retourne réel
# Retourne la plus grande des deux valeurs passées en paramètre
Variable plusGrand : réel
Début
Si a > b Alors
plusGrand <- a
Sinon
plusGrand <- b
FSi
Retourner plusGrand
Fin
Fonction compare(a : réel, b : réel) Retourne entier
# Retourne une valeur pour indiquer l'ordre des deux valeurs
# passées en paramètre
# 0 indique que les deux valeurs sont égales.
# 1 indique que la première valeur est la plus grande.
# -1 indique que la seconde valeur est la plus grande.
Variable ret : entier
Début
Si a = b Alors
ret <- 0
Sinon
Si a > b Alors
ret <- 1
Sinon
ret <- -1
FSi
FSi
Retourner ret
Fin
Algo TestFonctions
# Teste les fonctions compare et max
Variable val1, val2, maximum : réel
Variable rep : entier
Début
val1 <- saisir("Entrer une première valeur")
val2 <- saisir("Entrer une seconde valeur")
maximum <- max(val1, val2)
écrire("Le maximum de " & val1 & " et " & val2 & " est " & maximum)
rep <- compare(val1, val2)
Si rep = 0 Alors
écrire("Les deux valeurs sont égales")
Sinon
Si rep > 0 Alors
écrire("La première valeur est la plus grande")
Sinon
écrire("La seconde valeur est la plus grande")
FSi
FSi
Fin 2. Micro bataille navale (version 2)
Constante PLOUF... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

