Listes en C
Listes chaînées dynamiques
1. Qu’est-ce qu’une liste chaînée ?
a. Une chaîne constituée de maillons
Une liste chaînée est simplement une liste d’objets de même type dans laquelle chaque élément contient :
-
Des informations relatives au fonctionnement de l’application. Par exemple des noms et prénoms de personnes avec adresses et numéros de téléphone pour un carnet d’adresses.
-
L’adresse de l’élément suivant ou une marque de fin s’il n’y a pas de suivant. C’est ce lien via l’adresse de l’élément suivant contenue dans l’élément précédent qui fait la "chaîne" et permet de retrouver chaque élément de la liste.
L’adresse de l’objet suivant peut être :
-
Une adresse mémoire récupérée avec un pointeur (chaînage dynamique).
-
Un indice de tableau récupéré avec un entier.
-
Une position dans un fichier. C’est le numéro d’ordre de l’objet dans le fichier multiplié par la taille en octet du type de l’objet. Elle est récupérée avec un entier.
Que la liste chaînée soit bâtie avec des pointeurs ou des entiers, c’est toujours le terme de pointeur qui est utilisé : chaque élément "pointe" sur l’élément suivant, c’est-à-dire possède le moyen d’y accéder et une liste chaînée peut se représenter ainsi :

Chaque carré correspond à un maillon de la chaîne. Le petit carré noir en haut à gauche correspond à l’adresse en mémoire de l’élément. Le petit rond en bas à droite correspond au pointeur qui "pointe" sur le suivant, c’est-à-dire qui contient l’adresse de l’élément suivant. Au départ il y a le pointeur de tête qui contient l’adresse du premier élément, c’est-à-dire l’adresse de la chaîne.
b. Trois types de listes chaînées
Liste simple
La liste chaînée simple ne permet de circuler que dans un seul sens.
Liste symétrique ou doublement...
Piles
1. Principes de la pile
a. Modèle de données pile
La pile est une liste qui stocke de manière ordonnée les éléments. On peut l’assimiler à une pile d’assiettes : les assiettes à laver sont empilées les unes par-dessus les autres au fur et à mesure de leur arrivée et la personne qui lave les prend en commençant par le haut, ce qui fait que la dernière arrivée est la première lavée. De même, dans une pile informatique les éléments sont ajoutés un par un selon leur ordre d’arrivée et ils sont retirés un par un en partant du dernier arrivé appelé le sommet de la pile :
C’est la règle du dernier entré premier sorti : LIFO (Last In First Out).
b. Implémentation statique ou dynamique
Du point de vue de l’implémentation, une pile est une liste simplifiée qui n’accepte que des entrées-sorties en tête de liste. De même que pour les listes, il est possible d’avoir une pile en dynamique réalisée à la demande à l’aide de pointeurs ou une pile en mémoire contiguë réalisée selon une taille définie au départ avec un tableau.
Allocation dynamique de mémoire
Représentation d’une pile en dynamique :
Une pile en dynamique n’a pas de taille limite, hormis celle de la mémoire centrale (RAM) disponible.
Allocation contiguë de mémoire
Représentation d’une pile en contigu :
La taille d’une pile en contigu nécessite d’être spécifiée à un moment donné et gérée s’il s’agit d’un tableau dynamique.
Éventuellement il est envisageable d’avoir une pile sur fichier. Dans ce cas, la pile en contigu n’a plus de limite en taille. Mais l’écriture est plus lourde et les accès disque sont plus lents.
c. Primitives de gestion des piles
Les opérations de base effectuées sur les piles sont les suivantes :
-
Initialisation d’une pile : créer une pile vide.
-
Connaître si la pile est vide : renvoyer 1 si vrai 0 si non.
-
Connaître si la pile est pleine : renvoyer 1 si vrai 0 si non.
-
Lire l’élément sommet : récupérer les données...
Files
1. Principes de la file
a. Modèle de données file
La file est une liste qui stocke les éléments avec un ordre spécifique. C’est comme une file d’attente à la caisse d’un magasin. Les personnes arrivent une à une et constituent la file et elles partent une à une dans l’ordre d’arrivée après avoir payé. Il y a la personne en tête de file, la première et la personne en queue de file, la dernière. C’est l’ordre du premier arrivé premier sorti, "first in first out" dit FIFO en informatique :
b. Implémentation statique ou dynamique
Une file est une liste particulière qui utilise les deux côtés début et fin à la différence d’une pile qui n’en utilise qu’un. L’implémentation peut se faire en dynamique avec des pointeurs ou en contigu avec un tableau.
Allocation dynamique de mémoire
Représentation d’une file en dynamique :
Il est nécessaire d’avoir deux pointeurs pour une file : un pour gérer les entrées en queue et un pour gérer les sorties en tête. En dynamique une file n’a pas de taille limite, hormis celle de la mémoire centrale (RAM) disponible.
Allocation contiguë de mémoire
Représentation d’une file en contigu :
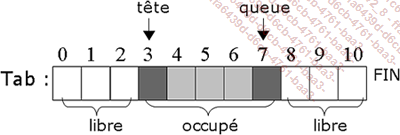
La gestion d’une file en contigu est moins aisée qu’elle n’en a l’air au premier abord. Il y a deux pointeurs d’indices, un pour la tête, un pour la queue mais il faut utiliser le tableau de façon circulaire. Les nouveaux entrants peuvent être placés au début ou à la fin selon la place restante dans le tableau. Si nous ajoutons 5 entrées et en supprimons 2 dans le schéma ci-dessus nous obtenons :

La taille d’une file en contigu nécessite d’être spécifiée à un moment donné et gérée s’il s’agit d’un tableau dynamique. Éventuellement il est envisageable d’avoir une file sur fichier. Dans ce cas la file en contigu n’a plus de limites en taille. Mais l’écriture est plus lourde et les accès disque sont plus lents.
c. Primitives de gestion des files
Les opérations de base effectuées...
Arbres
1. Généralités sur les arbres
a. Principe
Un arbre est une structure de données qui permet de stocker des informations mais aussi une hiérarchie et une organisation des informations :
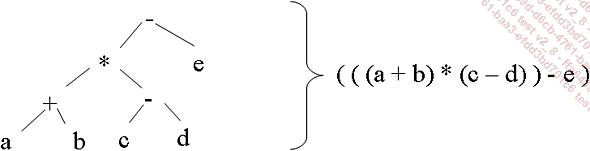
L’arbre est constitué de nœuds reliés entre eux de façon hiérarchique par des arrêtes. Le premier nœud est appelé racine, les derniers, ceux après lesquels il n’y a plus de nœud sont les feuilles. Un parcours de la racine vers une feuille est une branche. Chaque nœud peut être considéré comme la racine d’un sous-arbre constitué de sa descendance et de lui-même. L’arbre est de ce fait une structure récursive. Dans l’exemple ci-dessus chaque sous-arbre correspond à un parenthésage. Une information parenthésée peut traduire un arbre. L’expression : ( personne( nom, prénom, adresse( numéro, rue, ville, département) ) ) est celle de l’arbre :
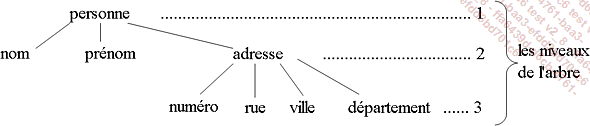
Chaque étage de l’arbre est appelé niveau et les niveaux sont numérotés de 1 la racine à n la feuille la plus basse. La hauteur d’un arbre est le niveau maximum atteint par une feuille. La hauteur de l’arbre ci-dessus est 3.
Souvent on parle de nœuds parents et de nœuds fils. Les nœuds fils sont ceux qui descendent d’un nœud parent et seule la racine n’a pas de parent. Dans l’exemple précédent, personne est la racine, il est parent de nom, prénom et adresse qui sont ses fils. Adresse est parent de numéro, rue, ville, département et numéro, rue, ville, département sont fils de adresse. Les fils d’un même parent sont frères.
b. Exemples d’utilisation des arbres
Expression arithmétique
Comme nous l’avons déjà mentionné, une expression arithmétique peut être représentée par un arbre. L’expression (a + b) * ( (c - d) / (e + f) ) donne l’arbre suivant :
Représentation de mots
Voici deux arbres : l’un pour représenter des mots qui commencent par m : mais, mars, mer, mon, et l’autre des mots qui commencent par s : sa, son, sel. Chaque branche de l’arbre constitue un mot. Ces arbres peuvent également se noter avec des parenthèses...
Contrôler un arbre binaire
1. Créer un arbre binaire
Les fonctions proposées ici permettent de créer des arbres soit à partir d’une description, soit de façon totalement aléatoire. Notre objectif est de les utiliser ensuite pour tester les fonctions de gestion des arbres.
a. Créer un arbre à partir d’un schéma descriptif
Voici l’arbre à créer :
Créer l’arbre "à la main", avec une fonction de création de nœud
Nous allons créer un arbre dynamique. Nous avons besoin d’un tableau de caractères pour stocker une chaîne (ou éventuellement juste un caractère puisqu’il n’y a que des caractères à stocker) et de deux pointeurs, un pour le fils gauche et un pour le fils droit. La structure de données est la suivante :
typedef struct noeud{
char dat[80];
struct noeud*g, *d;
}t_noeud;
Voici une fonction pour initialiser un nœud de l’arbre :
t_noeud* CN(char s[],t_noeud*g, t_noeud*d)
{
t_noeud*n;
n=(t_noeud*)malloc(sizeof(t_noeud));
strcpy(n->s, s);
n->g=g;
n->d=d;
return n;
}
et la fonction pour créer l’arbre :
t_noeud* creerArbre1()
{
return CN("A",
CN("B",
CN("D",NULL,NULL),
CN("E",NULL,NULL)),
CN("C",
CN("F",
CN("H",NULL,NULL),
NULL),
CN("G",NULL,NULL))
);
}
Cette méthode n’est pas pratique et des erreurs avec les parenthèses sont difficiles à éviter.
Créer l’arbre en utilisant sa description et un tableau
Autre possibilité, toutes les adresses des nœuds de l’arbre sont allouées et stockées dans un tableau et ensuite l’arbre est construit :
t_noeud* creerArbre2()
{
const int nbnoeud=9;
t_noeud**tab;
t_noeud*r;
int i;
// création du tableau de pointeurs
tab=(t_noeud**)malloc(sizeof(t_noeud*)*nbnoeud);
// allocation des adresses des noeuds
for (i=0; i<nbnoeud; i++)
tab[i]=(t_noeud*)malloc(sizeof(t_noeud));
// initialisation de chaque noeud en fonction du schéma de
// l'arbre ...Arbres binaires de recherche
1. Définition
Dans un arbre binaire de recherche, tous les éléments sont dotés d’une clé et ils sont positionnés dans l’arbre en fonction de cette clé. La clé rend lisible et utilisable l’ordre de l’arbre. La clé est en général un nombre qui est ajouté à l’élément. C’est grâce à ce nombre que l’élément peut être rangé et identifié à une place précise dans l’arbre. Tous les éléments peuvent ensuite être retrouvés rapidement grâce à leur clé, sans être obligés de parcourir tout l’arbre systématiquement. Les éléments rangés dans l’arbre sont en quelque sorte triés en fonction de leur clé. Il est facile d’ajouter des nouveaux éléments ou de supprimer des éléments sans modifier l’ordre de l’arbre.
Les clés obéissent aux règles suivantes :
Pour chaque nœud de l’arbre :
-
Les clés du sous-arbre gauche (SAG) sont inférieures à celle de la racine.
-
Les clés du sous-arbre droit (SAD) sont supérieures à celle de la racine.
-
Toutes les clés sont différentes, il n’y a pas de clé identique.
Par exemple la suite de clés 17, 3, 15, 9, 27, 44, 2, 50, 30 donne l’arbre suivant :
L’arbre ci-dessus suppose que les éléments sont entrés dans l’ordre de la suite, mais la forme de l’arbre dépend de l’ordre d’insertion :
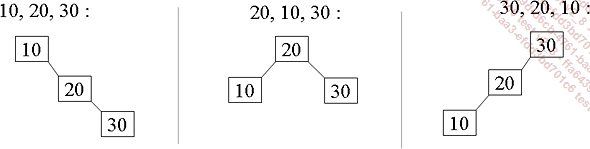
Remarque :
Quel que soit l’ordre d’entrée dans l’arbre des éléments avec leur clé, à l’issue, un parcours infixé de l’arbre donnera toujours une suite croissante des clés.
Ci-dessus ce sont les suites :
2, 3, 9, 15, 17, 27, 30, 44, 50
et
10, 20, 30
2. Structure de données
Notre objectif est de mettre en place un arbre binaire de recherche avec ses fonctions usuelles de traitement. Il s’agit d’un arbre dynamique. La clé peut être un entier mais souvent elle est intégrée au début d’une chaîne de caractères et nous allons prendre cette option pour...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
