Analyse numérique et maths opérationnelles
Calculs numériques dans l’esprit Matlab
1. Considérations pratiques
Dans ce chapitre, nous allons traiter de calculs numériques et d’expressions mathématiques souvent utilisées en machine learning ou par les ingénieurs. Ceci n’est ni un cours d’analyse numérique, ni un cours de mathématiques, ni un cours de mathématiques spécifiques au machine learning ; les savoirs y sont pour beaucoup exposés sur l’angle syntaxique et quand les explications sont plus détaillées, c’est dans l’optique de vous éviter une déconvenue lors de l’utilisation pratique des outils de calcul mis à votre disposition ici.
Attention, sauf mention contraire, dans la suite nous considérons nous trouver dans une base orthonormale d’un espace vectoriel euclidien (donc de dimension finie sur le corps des réels et muni d’un produit scalaire) et disposer d’une représentation dans cette base des objets que nous utiliserons (ou dans le système de coordonnées cartésiennes associées si cela a un sens).
Voici quelques rappels sur diverses caractéristiques calculatoires liées à cet état de fait (ces aspects ont déjà été évoqués sous une autre forme plus tôt dans l’ouvrage).
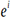 , si notre
espace vectoriel est muni du produit scalaire
, si notre
espace vectoriel est muni du produit scalaire 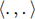 , un vecteur quelconque de l’espace
peut s’écrire comme suit :
, un vecteur quelconque de l’espace
peut s’écrire comme suit :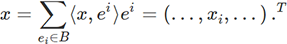
Le signe T, pour transposée, n’est pas utile à la définition, mais est là pour rappeler que nous adoptons traditionnellement une représentation des vecteurs en "colonne" (une colonne est très encombrante visuellement, donc on écrit une ligne et on transpose).
Souvent, on se contente de désigner par un "." le produit scalaire en question, d’où l’expression "dot" pour le désigner.
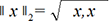 .
.Quand il n’y a pas d’ambiguïté, il est inutile de stipuler l’indice 2 en bas à droite des doubles barres.
Rappelons que pour construire un vecteur ligne en R, il suffit d’utiliser la fonction c(...). Illustrons ce calcul de norme euclidienne :...
Un peu d’algèbre linéaire
1. Exemple de création d’une base orthonormale
Nous nous proposons ici de créer une base orthonormale à partir d’une famille de vecteurs, puis de vérifier cette propriété. La base construite sera "au plus proche" de la famille d’origine. Nous attirons votre attention sur le fait que la famille en question génère un sous-espace vectoriel, mais n’en est pas explicitement une base.
À l’inverse, pour la simplicité de l’exemple R, nous considérons ici une famille de vecteurs formant déjà une base de l’ensemble de l’espace vectoriel considéré, mais on aurait pu traiter une famille générant un sous-espace de dimension inférieure et obtenir une base orthonormale de ce sous-espace, ce qui est en fait une des applications les plus naturelles de la fonction orth que nous allons utiliser.
Si vous n’êtes pas familier avec ces techniques, observez attentivement les manipulations de vecteurs colonnes. Elles sont rédigées de façon beaucoup moins compacte que dans les exemples que vous pourrez trouver ailleurs, mais vous permettront d’éviter de nombreuses erreurs pratiques lors de vos manipulations.
# famille de vecteurs, non orthonormée
v1 <- matrix(c(1,
1,
0), ncol = 1)
v2 <- matrix(c(0,
2,
0), ncol = 1)
v3 <- matrix(c(0,
0,
...Fonctions et systèmes d’équations, 1 à n variables
1. Fonctions d’une variable
a. Exploration de divers tracés
Nous disposons de nombreuses méthodes pour tracer des fonctions, abordons les plus simples. L’exercice de base est de tracer deux fonctions sur un même graphique. Ici les fonctions sont simples et naturellement vectorisées, n’oubliez pas de les vectoriser si besoin.
# définition des deux fonctions
f <- function(x){exp(-x)*sin(x)}
g <- function(x){exp(x)*sin(x)+1000} Avec R-base, la syntaxe est très simple.
curve(f,-10,10, col = "red", ylab = "f et g")
curve(g,-10,10, col = "blue", add = TRUE)
grid() 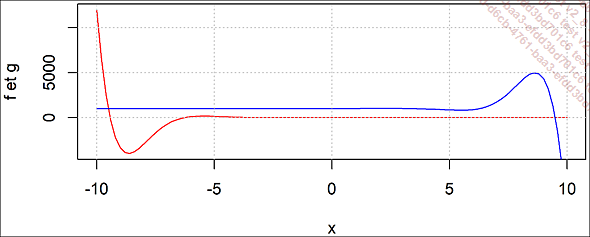
Deux fonctions
Nous allons introduire une méthode que nous avons déjà utilisée en début d’ouvrage, qui consiste à discrétiser les variables avant de les utiliser dans un graphique. Ce sera la façon de procéder quand on utilise pracma, ici au travers de sa fonction plotyy qui a pour objet de tracer deux courbes, mais avec des échelles, le cas échéant, différentes sur l’ordonnée, ce qui peut être très utile si l’on veut comparer l’allure de deux fonctions et surtout montrer leur éventuelle synchronisation ou désynchronisation sur l’axe des x.
x_ <- linspace(-10,10,100 + 1) # discrétisation de x via pracma::linspace
# -10 -9.8 ... 0 ... 9.8 10
plotyy(x_, f(x_), # f et g n'ont pas même échelle
x_, g(x_)) 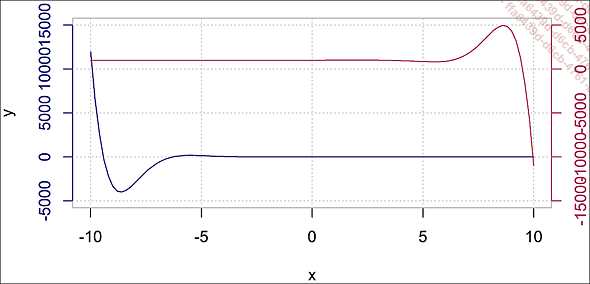
Deux fonctions mais deux échelles
Bien sûr, vous pourriez utiliser ggplot2 pour créer ce type de graphique, mais nous n’entrerons pas dans les détails des options puisqu’elles sont déjà évoquées plus haut dans l’ouvrage.
Voici une autre représentation possible, par facette, cette fois en ggplot2 :
f <- function(x){exp(-x)*sin(x)} # définir sa fonction
x_ <- linspace(-10,10,100 + 1) # discrétisation de x via pracma::linspace
...Dérivation de fonctions
Il existe diverses façons d’obtenir la dérivée d’une fonction en R. Tout d’abord, il convient de distinguer deux problèmes différents : voulons-nous calculer l’expression de cette dérivée, ce qui relève du calcul symbolique ? Ou voulons-nous obtenir la valeur de la dérivée de cette fonction en un point donné, ce qui relève de l’analyse numérique ? Notons que certains frameworks, comme TensorFlow, intègrent simultanément les deux approches pour obtenir une meilleure valeur numérique en un point et utilisent des algorithmes capables d’effectuer du calcul différentiel sur des fonctions elles-mêmes définies au travers d’un code informatique. On trouve souvent ce genre de technique sous le vocable AD pour Automatic Differentiation.
1. Dérivée symbolique et numérique avec R-base
Comme nous le savons déjà, il est aisé de calculer une dérivée symbolique simple avec les fonctions de base de R.
e <- expression(x^2+3*cos(x)- 1/x)
d <- D(e,'x')
d
##> 2 * x - 3 * sin(x) + 1/x^2 On pourrait l’évaluer par effet de bord de la façon suivante, mais ce n’est pas très "propre".
x <- pi
eval(d)
##> [1] 6.384506 Il est plus générique de construire une véritable fonction en insérant l’expression obtenue dans le corps de celle-ci via l’évaluation...
Autour de l’intégration
1. Calcul d’une intégrale multiple
Pour continuer cette démonstration comme quoi R est un biotope idéal pour les calculs scientifiques, considérons l’intégrale triple d’une fonction f sur un domaine D portant sur un élément de volume dV.
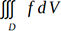
Dans un tel cas, f s’apparente souvent à une densité. Si f est la fonction unité, on obtient tout simplement le volume du domaine D.
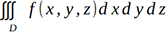 .
.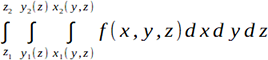 .
.Pour mémoire, notons que l’intégrale la plus imbriquée (sur dx) est une fonction de y et z et que l’intégrale sur dxdy est une fonction de z.
Nous allons utiliser la fonction permettant de calculer une telle intégrale avec le package pracma. Observez comment sont exprimées les limites du domaine que nous avons choisi comme exemple.
f <- function(x,y,z) x + y + 10*z # la fonction à intégrer
# définition du domaine D
z1 <- 0
z2 <- 1
y1 <- function(z) z
y1 <- Vectorize(y1) # vectorise y1, inutile dans ce cas, car y1 est très
...Fonctions spéciales et équations différentielles
1. Autres fonctions spéciales
Nous n’allons pas effectuer un cours, ni même une introduction mathématique à la notion de fonction spéciale, mais seulement attirer votre attention sur deux points :
-
ces fonctions se calculent souvent sur les réels et les complexes et donc leur représentation dans les complexes est plus difficile (typiquement, pour les visualiser dans le cas des complexes, on peut soit faire une coupe sur les réels ou les imaginaires, soit faire une représentation en 3D avec en x et y les axes réel et imaginaire et en z le résultat réel de la fonction… si l’on attend un réel !),
-
certaines de ces fonctions sont définies à partir d’une intégrale impropre avec des limites infinies ou des singularités dans la fonction à intégrer, ce qui rend cette intégration difficile (impossible avec une intégrale de Riemann). Ces problèmes sont globalement résolus au travers de différentes pratiques mathématiques qui s’appuient souvent sur des passages aux limites astucieux et extrêmement bien maîtrisés, ou des méthodes comme les valeurs principales de Cauchy (méthode qui s’applique aux singularités).
Ces fonctions spéciales ne sont pas évoquées ici parce qu’elles représenteraient des curiosités mathématiques, mais pour leur utilité dans de nombreux calculs pratiques, l’idée étant que vous ne soyez pas bloqué en voulant implémenter un calcul les utilisant trouvé au gré de vos lectures d’articles de recherche.
a. Fonctions d’Airy et de Bessel
Les deux fonctions d’Airy sont les solutions d’une équation différentielle difficile qui trouve son utilité dans divers domaines, dont la mécanique quantique (cas de l’équation de Schrödinger indépendante du temps), la mécanique des milieux continus (calcul du tenseur des contraintes de calculs d’élasticité dans un cas plan), la diffraction des ondes… Ces fonctions spéciales que l’on trouve dans Matlab n’étant pas disponibles dans pracma, il nous...
Éléments pratiques de calcul différentiel
1. Fonctions réelles d’un réel
Avant de rentrer dans le vif du sujet du calcul différentiel, nous allons à nouveau nous pencher sur les fonctions nous permettant de calculer une dérivée et introduire un peu de robustesse dans nos calculs de dérivées via pracma.
Nous considérons ici une fonction réelle d’un réel.
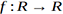
f <- Vectorize(function(x){exp(-x)*sin(x)+ x^3}) On peut obtenir sa dérivée première de nombreuses manières. Une des méthodes apportant la meilleure précision s’avère être la méthode "complex step", qui est peu sensible aux bruits liés à de nombreuses itérations et que l’on peut donc utiliser dans des algorithmes très itératifs.
complexstep(f,1) # dérivée robuste
##> [1] 2.889206 Le fait de disposer de résultats fonctions dérivées vectorisées nous permet de les appliquer membre à membre aux composants d’un vecteur quelconque.
complexstep(f,c(1,2,3)) # dérivée de chaque composante du vecteur
##> [1] 2.889206 11.820621 26.943685 On peut également utiliser la fonction fderiv, qui permet le cas échéant de dériver à gauche ou à droite du point considéré, ce qui peut être très utile quand la fonction n’est justement pas dérivable au point considéré. Par ailleurs, la fonction fderiv permet de calculer des dérivées d’ordre supérieur.
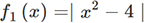 .
.f1 <- function(x) abs(x^2-4)
curve(f1, -4, +4); grid() 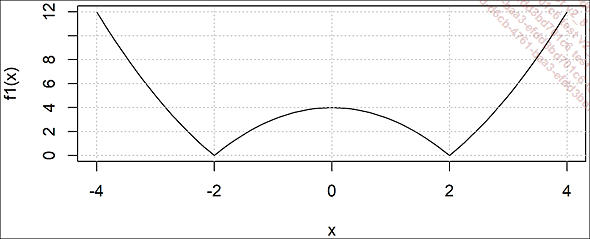
Courbe non dérivable en tous points
Pourtant, si vous essayez de la dériver en ce point, vous obtiendrez un résultat (faux !) :
fderiv(f1,2) # résultat trompeur
##> [1] 6.055514e-06 En fait, il fallait calculer la dérivée à gauche et à droite :
fderiv(f1, 2, method = "backward") # à gauche
##> [1] -4
fderiv(f1, 2, method = "forward") # à droite
##>...Calcul symbolique avec SymPy
SymPy est une librairie Python accessible en R. Le package R permet divers calculs symboliques qui peuvent vous permettre de gagner beaucoup de temps, comme par exemple dans la simplification d’une expression mathématique ou dans l’expression d’une dérivée ou d’une limite.
SymPy est l’outil Python de référence pour effectuer des calculs symboliques simples. Son installation en Python peut poser quelques difficultés, mais elle est en général facile sous R, car elle s’effectue via l’installation du package rSymPy (en stipulant que l’on veut toutes les dépendances).
Comme d’habitude, il faut faire :
library(rSymPy) Attention, les dépendances de ce package sont inattendues : rJython (un Python sous Java auquel on accède via R), rJava (Java sous R, qui nécessite l’installation de Java) et rjson.
Effectuons quelques calculs symboliques simples pour tester :
x <- Var("x") # Ne pas oublier les ""
x+3*x
##> [1] "4*x"
x/x
##> [1] "1"
y <-Var("x**3")
y/x
##> [1] "x**2" Voici un exemple de calcul de limite :
sympy("limit(x/exp(x), x, oo)")
##>... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations


