Maîtriser les bases
Se mettre en harmonie avec les données
L’erreur la plus commune des personnes fraîchement initiées aux data sciences s’avère être l’utilisation directe, sans précaution et sans analyse préliminaire des algorithmes à leur disposition sur des données incomprises.
Tout au long du processus d’élaboration de son étude et a fortiori dès son premier contact avec un problème, le data scientist aura intérêt à évaluer ses données au travers de divers outils statistiques et à visualiser celles-ci sous divers points de vue. C’est à ce prix que l’on peut émettre des hypothèses judicieuses que l’on cherchera à valider ou à invalider tout au long du processus.
Le lecteur intéressé qui voudrait revenir aux sources aura sans doute beaucoup de plaisir à parcourir l’œuvre d’Andrei Kolmogorov à qui nous devons de nombreuses contributions à certains concepts sous-jacents à notre pratique des data sciences (formalisation de la logique intuitionniste comme étant du "calcul sur des problèmes", loi forte des grands nombres, axiomatisation des probabilités au travers du langage des théories de la mesure, upsilon-entropie qui nous permet de qualifier les estimateurs, application de la méthode de Poincaré à l’étude des équilibres...).
L’interprétation des outils statistiques nécessite l’assimilation de quelques notions fondatrices autour des probabilités que nous allons aborder maintenant.
1. Quelques notions fondatrices
a. Phénomène aléatoire
Vous vous trouvez face à un phénomène aléatoire si, quand vous effectuez une expérience plusieurs fois dans des conditions identiques, vous obtenez des résultats différents (et donc d’une certaine manière... imprévisibles).
Remarquez que dans cette définition, le fait qu’un phénomène soit identifié comme aléatoire dépend de l’incapacité de l’observateur à le prévoir complètement, ce qui lui fera déclarer de façon péremptoire que le phénomène...
Matrices et vecteurs
1. Conventions, notations, utilisations basiques
Cette section n’a pas d’autre prétention que de vous familiariser avec l’utilisation pratique des matrices et des vecteurs, telle qu’elle est le plus souvent présentée dans cet ouvrage. L’aspect mathématique sous-jacent n’est pas pris en compte (ou peu pris en compte).
Fabriquons une matrice
Supposez un dataset composé de lignes (par exemple représentant des évènements ou des individus) et dont les colonnes représentent les valeurs pour chaque attribut (en anglais feature). Une ligne décrivant un individu nommé Robert, d’âge 40 ans, de statut marié et habitant dans la ville Paris pourrait être encodée de la façon suivante dans un tableau avec d’autres individus :
!nom ! âge ! statut ! ville !
! ! ! ! !
!ROBERT ! 40! M ! PARIS !
!PHILIPPE ! 30! C ! LYON !
!RODOLF ! 20! C ! LYON !
!MARIE ! 35! M ! PARIS ! Si l’on mémorise le numéro de ligne de chaque individu :
!nom ! ligne !
! ! !
!ROBERT ! 1 !
!PHILIPPE ! 2 !
!RODOLF ! 3 !
!MARIE ! 4 ! Si on encode le statut de la façon suivante : "M" vaut 1 et "C" vaut 0, puis si on remplace la ville par son code postal, on peut obtenir un tableau de chiffres ayant la même signification :
! ligne ! âge ! statut ! ville !
! ! ! ! !
! 1 ! 40! 1 ! 75000 !
! 2 ! ...Estimations
1. Positionnement du problème d’estimation
a. Formulation générale du problème
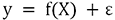 .
.Dans le cas courant, un grand nombre des éléments du vecteur y est inconnu, l’application f() est à déterminer et le vecteur d’erreur est supposé avoir une moyenne à 0 et une norme petite par rapport à la norme de y.
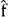 et une estimation de y que nous noterons
et une estimation de y que nous noterons 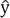 tels que
tels que 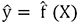 .
.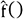 telle qu’une "forme"
d’écart entre
telle qu’une "forme"
d’écart entre 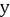 et
et 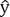 soit minimum.
soit minimum.Pour exprimer l’écart global à minimiser, on se dote d’une application pour mesurer l’écart ou "perte" (loss en anglais). L’écart est calculé entre une valeur connue et une valeur estimée pour une observation donnée.
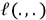 cette application qui, dans le cas où les
yi sont des valeurs de
cette application qui, dans le cas où les
yi sont des valeurs de 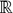 , est une application de
, est une application de 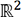 vers
vers 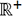 .
.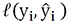 pourrait
naturellement prendre la forme d’une distance induite par une norme
ou d’une fonction monotone sur
pourrait
naturellement prendre la forme d’une distance induite par une norme
ou d’une fonction monotone sur 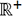 d’une distance induite par une norme.
d’une distance induite par une norme.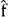 telle que la moyenne des
telle que la moyenne des 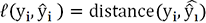 soit minimum, ou que la moyenne de leurs carrés
le soit (notez que nous n’avons pas défini ici la distance
choisie).
soit minimum, ou que la moyenne de leurs carrés
le soit (notez que nous n’avons pas défini ici la distance
choisie).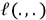 soit minimum.
soit minimum.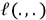 .
.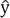 par sa valeur et en notant la moyenne sur les
observations du training set par < >T :
par sa valeur et en notant la moyenne sur les
observations du training set par < >T : 
Mise en pratique : apprentissage supervisé
Nous allons effectuer un petit cycle de construction d’une prédiction afin de mettre en pratique les notions vues précédemment. Tout d’abord nous allons nous doter d’un ensemble d’observations. Cet ensemble comportera 10 000 observations, deux features en entrée et une à prédire. On cherchera le modèle f, la feature cible étant y, l’entrée étant X(x1,x2). L’ensemble des observations Z=(X,y) est scindé en un ensemble d’entraînement Ze de 6 000 lignes et un ensemble de validation Zv de 4 000 lignes.
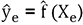
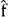 sur l’ensemble de validation Xv et
nous obtiendrons un vecteur de prédictions
sur l’ensemble de validation Xv et
nous obtiendrons un vecteur de prédictions 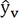 que nous comparerons avec le vecteur yv des
valeurs réelles issues de l’ensemble de validation.
que nous comparerons avec le vecteur yv des
valeurs réelles issues de l’ensemble de validation.Pour ce faire, nous allons créer un ensemble Z "factice" où nous avons imposé, puis perturbé aléatoirement le fait que y soit plus ou moins situé sur le plan 2 . x1 - 7 . x2 + 1.
Notre espoir est de constater que les algorithmes utilisés retrouvent l’équation de ce plan avec une erreur de faible amplitude.
1. Préparation
Le code de création de l’ensemble factice d’observation est le suivant (sans intérêt spécifique) :
# un dataset factice, création des matrices #
rm(list=ls())
g <- function(x){s <- round(abs(sin(x)*1000 ))
set.seed(s) # randomize
# mais assure que g(constante) est une constante
x*(1- 0.5*rnorm(1)*sin(x))} # pour perturber
set.seed(2); x1 <- matrix(rnorm(10000))
set.seed(3); x2 <- matrix(rnorm(10000))
y <- matrix(2*x1-7*x2+1)
y ... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations


