Autres problèmes, autres solutions
Séries temporelles
Quand des observations évoluent dans le temps, nous les modélisons au travers d’une série temporelle et vérifions si sa séquentialité influence les valeurs des observations.
1. Introduction
Les séries temporelles ont pour variable sous-jacente une variable temporelle. On peut les considérer comme l’extension d’une liste d’observations indexées par une variable temporelle. À la limite, si les intervalles de temps tendent vers 0, la variable temps qui était discrète peut être définie comme continue. Dans ce cas, on considère la série discrète correspondante comme une série d’observations possibles de la série continue, qui s’avère souvent représenter un système physique (une oscillation, un signal électronique ou biologique ou par extension le cours d’indices boursiers...).
L’étude des séries temporelles se base sur l’a priori que chaque valeur de la série dépend d’autres valeurs de la série, le plus souvent de valeurs précédentes. Dans ce dernier cas, on tente naturellement d’exprimer cette dépendance au travers d’une fonction. Cette fonction peut être perçue comme une fonction génératrice de la série qui s’applique sur un ensemble de premiers éléments.
Dans cette mesure, il est compréhensible que l’on nomme aussi ces séries "processus".
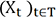 définies sur un même espace
probabilisé.
définies sur un même espace
probabilisé.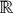 .
.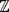 , ce qui exprime également que l’on
ne préjuge pas de l’existence d’un début
au processus. Dans la pratique, on effectue une restriction de T à un
ensemble fini d’indices I inclus dans l’ensemble des entiers naturels
positifs
, ce qui exprime également que l’on
ne préjuge pas de l’existence d’un début
au processus. Dans la pratique, on effectue une restriction de T à un
ensemble fini d’indices I inclus dans l’ensemble des entiers naturels
positifs 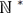 . On effectue...
. On effectue...Systèmes flous
1. Introduction
Cette section introduit des notions que vous retrouvez dans différents algorithmes et différents packages. Celui-ci vous permettra d’aborder divers sujets dans d’autres contextes, en particulier celui des systèmes experts. Ces systèmes semblent passés de mode hors du monde industriel, mais nous avons la conviction que ceux-ci reviendront bientôt en force dans l’outillage des data scientists futurs.
Le fait que les systèmes flous (fuzzy systems) s’avèrent efficaces dans la reconnaissance de patterns et l’approximation de fonctions "complexes" provient en partie de leur capacité à supporter une codification efficace des connaissances.
Les systèmes flous se basent sur des systèmes experts à base de règles (rule-based systems) ayant souvent l’aspect suivant : "SI ceci ALORS cela".
Comme le laisse supposer le terme "fuzzy", ces règles sont de plus entachées d’une logique floue (via l’incorporation de la notion d’ensembles flous - les fuzzy sets que nous allons aborder plus bas).
Un ensemble flou peut être compris comme étant le couple formé par un ensemble "classique" (en anglais crisp) et une fonction sur les éléments de cet ensemble prenant ses valeurs dans un certain intervalle, typiquement [0,1]. Cette fonction quantifie la vraisemblance d’une assertion (c’est en fait le niveau d’appartenance à l’ensemble, une extension de la notion de "fonction caractéristique" qui vaut 0 quand un élément n’est pas dans l’ensemble et 1 quand l’élément est dans l’ensemble).
La facilité d’interprétation des règles par les humains aide à la mise au point de ces systèmes, en particulier si le nombre de règles reste raisonnable. La codification d’une connaissance incertaine y est possible, ce qui améliore le dialogue avec les experts car il n’est pas nécessaire de capter toute sa connaissance sur un sujet au travers d’une seule règle très complexe et exprimée en une seule fois. Au contraire, on empilera des règles unitaires annotées de leur incertitude, si bien que la validation individuelle...
Essaim (swarm)
Les analogies avec la nature inspirent les créateurs d’algorithmes. Quand on regarde l’action d’une colonie de fourmis (ant) qui va chercher de la nourriture sur une nappe lors d’un déjeuner sur l’herbe, on est surpris de "l’intelligence collective des fourmis". Celles-ci s’organisent en files vers les points où elles trouvent le plus de ressources, explorent avec efficacité le territoire, changent leur comportement et leur organisation quand on ajoute des obstacles et changent leur organisation quand une ressource vient à manquer à un endroit de la nappe.
L’idée des algorithmes qui utilisent cette analogie est simple : il n’y a pas d’intelligence centralisée dans ces comportements, mais la conjonction de comportements faciles à coder (c’est-à-dire peu intelligents) et d’échanges d’informations succincts confine une certaine intelligence collective à l’essaim (swarm).
1. Swarm et optimisation : l’algorithme PSO
L’usage le plus courant de tels algorithmes est la recherche d’optimum dans le cas de problèmes très difficiles, typiquement quand il existe de nombreux optimums locaux. Remarquez que le fait de trouver ces optimums locaux peut faire partie de nos objectifs, au même titre que nos fourmis ne recherchent pas uniquement la plus grande source de nourriture, mais toutes les sources de nourritures notables accessibles à une certaine distance de leur base.
a. Présentation de PSO
L’algorithme PSO (Particle Swarm Optimization) met en œuvre une population de particules qui se déplacent de façon stochastique dans l’espace de recherche. Chaque individu est caractérisé par sa meilleure performance dans cet espace (par exemple, là où la fourmi a trouvé le plus de nourriture, et non pas là où se trouve réellement le plus de nourriture). L’individu communique cette expérience à une certaine partie de la population (suivant ses moyens de communication et en fait suivant votre volonté de programmeur !). Il est parfois plus judicieux de ne communiquer l’information qu’à un ensemble restreint de la population pour ne pas déformer le comportement de tout l’essaim....
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations


