L’état quantique
Vers une définition de l’état quantique
1. Le principe d’incertitude d’Heisenberg
Ce principe édicté par le physicien allemand Werner Heisenberg (1901 -1976) stipule qu’il est impossible de connaître simultanément, deux grandeurs d’une particule (dans le monde quantique bien sûr). Par exemple, si on connaît la vitesse de la particule, il sera difficile de connaître sa position et vice versa. Plus exactement, si on connaît avec précision la vitesse on aura une valeur d’une grande incertitude de la position de la particule. On appelle parfois ce principe, le principe d’indétermination.
2. La mesure quantique
Avant même de préciser ce qu’est un état quantique, il faut sans doute apporter quelques précisions quant à la mesure de cet état quantique.
Par exemple, supposons que nous souhaitions mesurer un état quantique. Eh bien, cette mesure aurait pour effet immédiat d’interrompre la dualité onde-corpuscule et donc de faire cesser la caractérisation quantique du système étudié. La mesure obtenue serait une mesure de la mécanique classique.
En d’autres termes, un comportement quantique cesse dès lors qu’on le mesure. C’est comme si toutes ses caractéristiques quantiques disparaissaient dès lors que l’on cherche...
L’état quantique et les mathématiques
1. Rapide retour sur les vecteurs
L’état quantique est éminemment mathématique. Plus généralement, la physique quantique étant tellement contre-intuitive qu’elle est devenue un terrain privilégié de formalisme mathématique. Comme annoncé, l’essentiel sera expliqué ici ; nombre de concepts quantiques étant en effet explicables, à défaut d’être démontrables, avec le langage naturel.
Toujours est-il que l’état quantique va être représenté par « une sorte de vecteur » comme nous allons le voir rapidement. Nous devons donc faire un rapide retour sur la notion même de vecteur. Considérons pour cela l’échiquier suivant sur lequel se trouve un cavalier :
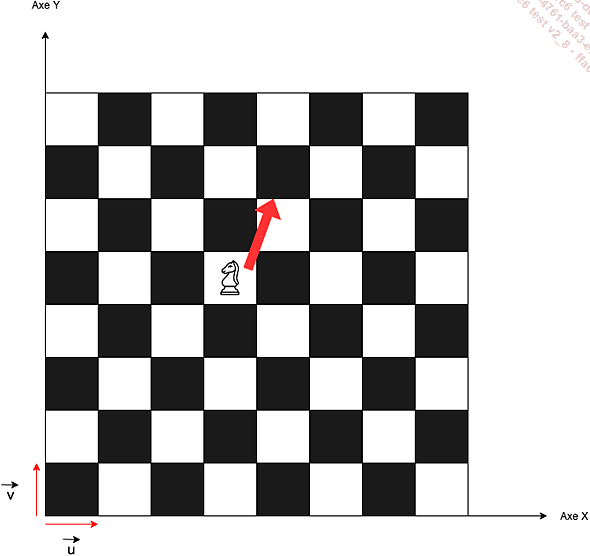
Illustration 1 : représentation vectorielle d’un déplacement d’une pièce aux échecs
On voit que l’échiquier est muni d’un repère (X, Y). Si l’on suppose que ce repère est orthonormé et qu’à chaque case correspond une unité de longueur dans chacune des deux directions, on peut dire que la position courante du cavalier est :
-
égale à c représentant les coordonnées du cavalier dans le repère (X, Y)
-
On a alors :
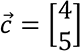
Fonction d’onde
1. La mise en évidence graphique
Si on poursuit l’exemple précédent, on peut à présent représenter graphiquement cette dernière équation en mettant en évidence les différentes valeurs possibles après mesure.
On appelle ici une fonction discrète, une fonction qui n’est justement pas continue et dont la prise de valeurs correspond à une discrétisation.
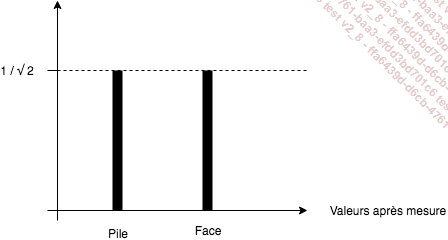
Illustration 3 : fonction d’onde discrète
Cette représentation graphique et discrète s’appelle fonction d’onde en physique quantique. Sur le plan du vocabulaire, le fait d’atteindre telle ou telle valeur après mesure s’appelle la réduction du paquet d’ondes, car il est justement « réduit » à une seule valeur (ici « pile » ou « face »).
2. La fonction d’onde continue
Nous venons de voir une fonction d’onde discrète, mais elle peut tout à fait être continue. Par ailleurs, on peut élever au carré la fonction d’onde pour accéder à la probabilité de chaque valeur possible. On appelle cette seconde fonction fonction de densité.
Ainsi, dans l’exemple graphique suivant, on affiche une fonction d’onde et sa fonction de densité associée.
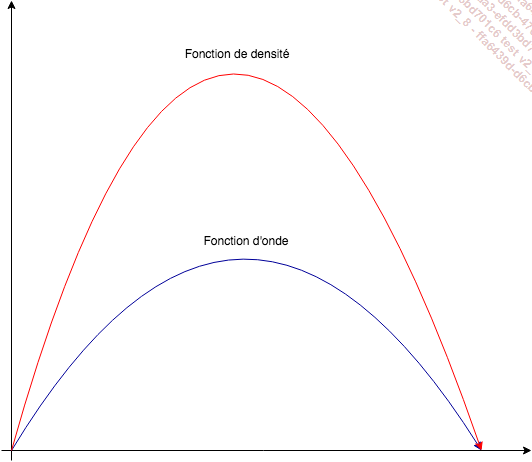
Illustration...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
