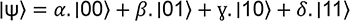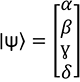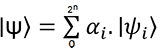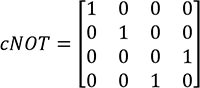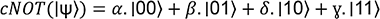La porte quantique
Comparaison avec l’informatique quantique
1. Introduction
En informatique dite classique, l’informatique telle que nous la connaissons, utilise un ordinateur classique utilisant des bits c’est-à-dire des valeurs prenant des « 0 » ou des « 1 ». L’ensemble des actions effectuées sur un ordinateur correspond en effet à des opérations de bits. Ces opérations sont réalisées à l’aide de portes logiques qui permettent de faire des opérations sur un ou plusieurs bits. Ces portes logiques sont conçues au niveau de l’infrastructure avec des transistors. Un ordinateur personnel et son micro-processeur contiennent des millions de transistors.
2. Exemple de la porte logique NOT
Pour commencer à fixer les idées en vue de l’apprentissage des portes quantiques, prenons un premier exemple de porte logique, en l’occurrence la fonction NON et donc la porte logique NOT.
On commence par proposer la table de vérité qui propose les différents scénarios de la porte logique. Par exemple « S’il y a telle valeur en entrée alors on aura telle valeur en sortie » :
|
entrée |
sortie |
|
0 |
1 |
|
1 |
0 |
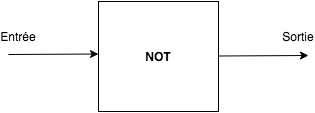
Illustration 1 : représentation de la porte logique NOT (non normalisée)
Ainsi, quand on envoie un bit de valeur 0 en entrée, on obtient...
Les portes quantiques à un qubit en entrée
1. Introduction
De manière un peu similaire, on va avoir ce type de schéma qui fait passer un bit quantique et son état quantique à un autre état grâce au passage dans une porte quantique, c’est-à-dire une sorte de brique à même de faire évoluer l’état :
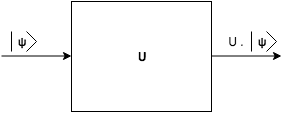
Illustration 3 : représentation d’une porte quantique
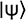 un nouvel état
un nouvel état 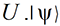 ; U représente la matrice de passage d’un état à l’autre.
; U représente la matrice de passage d’un état à l’autre.Pour rappel, un bit quantique peut se représenter de manière vectorielle. Si on a un état quantique défini à partir de deux bits quantiques, alors on a cet état tel que :
Donc l’état quantique peut s’exprimer de manière vectorielle, ainsi :
C’est ce vecteur qui sera soumis au calcul matriciel associé à la porte quantique.
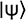 est définit selon n qubits, alors l’état
quantique sera défini comme une combinaison linéaire
dans une base vectorielle de dimension 2n :
est définit selon n qubits, alors l’état
quantique sera défini comme une combinaison linéaire
dans une base vectorielle de dimension 2n :On a donc un vecteur de taille 2n pour représenter cet état quantique.
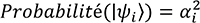 ;
cette propriété va d’ailleurs être mise
en œuvre dès l’étude de la première
porte quantique.
;
cette propriété va d’ailleurs être mise
en œuvre dès l’étude de la première
porte quantique.2. Porte de Hadamard (H)
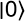 et
et 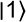 alors qu’en
entrée on a un qubit dans un état non superposé.
On souhaite en effet qu’il y ait autant de chances après
mesure d’atteindre
alors qu’en
entrée on a un qubit dans un état non superposé.
On souhaite en effet qu’il y ait autant de chances après
mesure d’atteindre 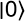 que de chances
d’atteindre
que de chances
d’atteindre 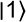 :
:-
On souhaite donc que :...
Les portes quantiques à deux qubits en entrée
1. Introduction
La section précédente a présenté la notion de porte quantique et a inventorié les principales portes quantiques à un bit quantique en entrée. Le présent sous-chapitre se concentre sur les portes quantiques prenant deux bits quantiques en entrée. En l’occurrence, les portes quantiques à deux entrées ont un nombre variable de sorties selon la porte considérée : une, deux ou plus de sorties.
2. Porte cNOT (cX)
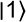 ; dans tous les autres cas, le second bit quantique
est laissé inchangé. On nomme ainsi le premier
bit quantique d’entrée qubit de contrôle.
Le second est en général nommé qubit cible. Cette porte quantique
est notamment utilisée pour implémenter l’intrication
quantique entre le qubit cible et l’un des qubits de sortie.
; dans tous les autres cas, le second bit quantique
est laissé inchangé. On nomme ainsi le premier
bit quantique d’entrée qubit de contrôle.
Le second est en général nommé qubit cible. Cette porte quantique
est notamment utilisée pour implémenter l’intrication
quantique entre le qubit cible et l’un des qubits de sortie.De façon similaire, il existe les portes cY et cZ non détaillées ici, car peu ou pas utilisées dans la suite de l’ouvrage.
La porte cNOT a la matrice de transformation suivante :
-
-
Ainsi soit
alors :
La représentation graphique de la porte...
Les portes quantiques à trois qubits en entrée
1. Porte TOF (CCNOT)
La porte TOF, de son nom complet porte de Toffoli, a été conçue en 1980 par le scientifique italien Tommaso Toffoli. Elle consiste en une porte quantique prenant trois bits quantiques en entrée. On lui donne parfois le nom de « CCNOT » comme Controlled controlled NOT.
Controlled controlled NOT s’entend ainsi : un premier qubit de contrôle, contrôle un second qubit de contrôle qui lui-même contrôle le troisième qubit, le bit quantique cible.
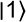 alors la porte NOT (la porte de Pauli-X) est
appliquée au troisième bit quantique d’entrée.
alors la porte NOT (la porte de Pauli-X) est
appliquée au troisième bit quantique d’entrée.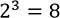 :
:Le schéma associé est sans surprise le suivant :
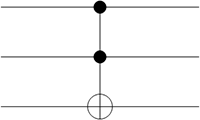
Illustration 10 : représentation de la porte TOF (CCNOT)
2. Porte Fredkin (CSWAP)
La porte Fredkin est, elle aussi, une porte à trois qubits d’entrée. Elle porte le nom du physicien américain Edward Fredkin. Elle est parfois surnommée « CSWAP », c’est-à-dire controlled swap ; on ajoute donc un qubit de contrôle à une porte SWAP telle qu’étudiée précédemment.
Le schéma...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations