Comprendre l'informatique quantique
Quelques définitions
1. Représentation des états quantiques
a. La superposition quantique
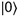 et
et 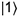 (figure 7).
(figure 7).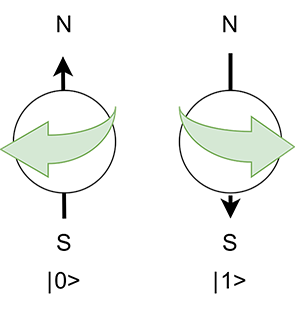
Figure 7
Dans l’expérience de Young, l’électron se trouve dans une superposition de deux états différents. Les pôles magnétiques des deux états sont inversés l’un par rapport à l’autre, ce qui conduit à un sens de « rotation » différent.
Le terme « rotation » vient ici entre guillemets, car il relève du domaine de la mécanique classique. Le terme adéquat est « spin ».
|
Encadré 2 La notion de spin a été définie par le physicien autrichien Wolfgang Pauli en 1924. Ce physicien a joué un rôle significatif dans le développement de la théorie quantique (cf. section Quelques définitions, sous-section Les portes de Pauli de ce chapitre). Le spin est une propriété que possèdent les particules, tout comme la masse ou la charge électrique. Par exemple, un électron possède une charge négative de 1,6 x 10^-19, une masse d’environ 9 x 10^-30 kilogramme, et un spin de 1/2. Bien que nous utilisions fréquemment le terme « rotation » pour décrire le spin, ce terme n’est pas tout à fait approprié. Strictement parlant, le spin correspond à un moment cinétique, encore appelé moment angulaire. Pour mieux comprendre le concept de moment cinétique, imaginez-vous en train de pousser une porte. Si vous poussez la porte près de ses charnières, il est difficile de la faire bouger. En revanche, si vous appliquez la même force au niveau de la poignée, la porte s’ouvre plus facilement. La force appliquée est la même dans les deux cas, mais le moment de force diffère. C’est comparable au principe du bras de levier. Comme... |
Qu’est-ce que l’intrication quantique ?
Dans l’expérience du chat de Schrödinger, l’état du chat est lié à celui de l’atome (désintégré ou non). Les deux entités, en l’occurrence le chat et l’atome, sont intriquées. Autrement dit, l’intrication est un phénomène dans lequel deux (ou plusieurs) entités partagent une ou plusieurs propriétés.
La métaphore s’arrête cependant ici, car l’intrication inclut également une notion de distance : peu importe la distance qui sépare les entités intriquées, si l’une des entités change, alors l’autre change également. Cela n’est pas forcément le cas du chat de Schrödinger, dans la mesure où sa mort pourrait survenir de façon plus ou moins rapide selon la distance qui le sépare du dispositif censé le tuer.
Un contre-exemple intuitif serait une ampoule connectée à un interrupteur Bluetooth. L’état de l’ampoule (allumé ou éteint) dépend du statut de l’interrupteur (ouvert ou fermé). Cependant, il suffit d’éloigner suffisamment l’interrupteur de l’ampoule, dans une pièce assez distante par exemple, pour que les deux états ne soient plus liés, la connexion Bluetooth étant perdue.
En jargon un peu technique, on dit que l’intrication viole le principe de localité de Bell, qui énonce que deux entités distantes ne peuvent s’influencer instantanément. Le principe de localité fait partie des hypothèses fondatrices des inégalités de Bell. L’intrication transgresse en totalité ce principe de localité, invalidant de ce fait les inégalités de Bell (détaillées dans l’encadré 9). C’est ce que démontre le travail expérimental extrêmement pointu d’Alain Aspect qui lui a valu le prix Nobel de physique en 2022.
|
Encadré 9 Paradoxe EPR (du nom de ses découvreurs : Einstein, Podolsky et Rosen) Le formalisme quantique suggère que deux particules peuvent échanger des informations instantanément, indépendamment de la distance... |
Qu’est-ce que la téléportation quantique ?
Revenons sur le paradoxe EPR (encadré 9) et sur le concept d’action fantomatique à distance. Alice et Bob, deux scientifiques imaginaires, possèdent chacun un membre d’une paire de qubits, préalablement intriqués. Lorsque Alice modifie l’état de son qubit, alors le qubit de Bob subit la même opération. En modifiant l’état de son qubit, Alice transmet donc une information à Bob. C’est là toute l’idée des protocoles de téléportation quantique : utiliser une paire de qubits intriqués comme un canal pour transmettre des informations entre Alice et Bob.
1. Le théorème de non-clonage
Dans une excellente introduction à l’informatique quantique, Michael A. Nielsen et Isaac L. Chuang [15] présentent le théorème du non-clonage de la façon suivante.
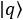 à cloner et d’une page blanche
à cloner et d’une page blanche 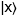 , de produire
, de produire 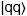 en sortie.
en sortie.Dans leur article, Nielson et Chuang parlent, non pas d’une photocopieuse, mais d’une machine quantique. L’idée de la photocopieuse vient d’une interprétation livrée par l’utilisateur Invite73192618 le 22/08/2011 sur le forum futura-sciences : https://forums.futura-sciences.com/physique/492135-theoreme-de-non-clonage.html.
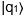 et
et 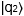 , deux états quantiques quelconques à cloner.
Formellement, nous avons donc :
, deux états quantiques quelconques à cloner.
Formellement, nous avons donc :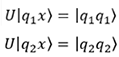
Prenons maintenant le produit scalaire des deux équations précédentes :
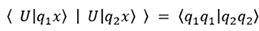
 et
et  . Faire une
photocopie de
. Faire une
photocopie de 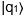 et
et 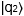 ne modifie pas cette différence. Autrement
dit, nous avons :
ne modifie pas cette différence. Autrement
dit, nous avons :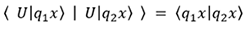
Nous trouvons donc que :
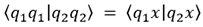
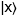 sont
sont 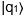 et
et 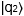 . Posons,
par exemple. Alors :
. Posons,
par exemple. Alors :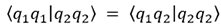
Pour rappel, le produit...
Cas pratique : exécuter un programme quantique
Ce cas pratique vise à mettre à profit les connaissances acquises dans ce chapitre. Il s’agit de transporter une information d’Alice vers Bob grâce à la téléportation quantique. Pour cela, vous aurez besoin de Qiskit (https://qiskit.org/). Cette librairie développée par IBM permet de réaliser des calculs quantiques. Cet exercice reprend d’ailleurs en partie, mais de façon simplifiée, le tutoriel de Qiskit (https://learn.qiskit.org/course/ch-algorithms/quantum-teleportation).
1. Mise en place de l’environnement de développement
Vous allez utiliser IBM Quantum Lab (https://lab.quantum-computing.ibm.com/), qui est une plateforme cloud gratuite basée sur Jupyter (https://jupyter.org/).
Jupyter est une console interactive (notebook) qui permet d’afficher des images, des tables, de zoomer, de cliquer, de garder en mémoire des résultats, etc.
IBM Quantum Lab contient une base de données d’exemples sous forme de notebooks. Ils sont accessibles à tous. En outre, Qiskit est installé par défaut dans l’environnement des notebooks créés sur IBM Quantum Lab.
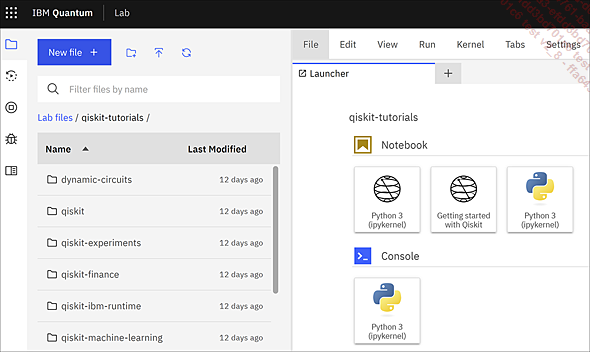
Figure 26
Écran d’accueil d’IBM Quantum Lab. Un certain nombre de notebook-exemples sont déjà présents dans l’explorateur de fichiers à gauche.
Il est bien sûr possible d’utiliser Qiskit localement. Pour ce faire, suivez ces étapes :
Installez un gestionnaire d’environnement. Anaconda est conseillé (https://www.anaconda.com/).
Créez un environnement Python. Pour créer l’environnement my_test avec Python 3.9, utilisez le prompt d’Anaconda et entrez cette commande :
conda create... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
