Conclusion
Résumé du livre
Nous allons revoir brièvement les points-clés abordés dans ce livre, depuis l’expérience de Thomas Young, jusqu’à la décohérence quantique et aux enjeux de la recherche en informatique quantique.
1. De la physique à l’informatique quantique : les promesses
L’informatique quantique est un domaine dont les fondements sont ancrés dans la physique quantique. Elle repose sur la propriété onde-corpuscule des objets à une échelle suffisamment petite. Dans l’expérience de Thomas Young, considérée comme un précurseur de la physique quantique, une particule se présentant face à deux fentes se comporte « comme si elle passait par les deux fentes en même temps ». Cette particularité ouvre la voie à une puissance de calcul décuplée, potentiellement supérieure à celle des ordinateurs classiques. Les applications de l’informatique quantique sont prometteuses, en particulier dans le domaine de la sécurité et de l’optimisation dite combinatoire (les problèmes d’optimisation combinatoires sont caractérisés par un grand nombre de solutions possibles). L’informatique quantique peut être utilisée entre autres en pharmacologie pour trouver la meilleure forme d’une molécule, parmi un ensemble de molécules ayant des propriétés médicamenteuses similaires.
2. Superposition et mesure
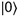 et
et 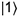 . C’est le phénomène
de superposition. Par analogie avec l’informatique classique, nous appelons
qubit l’unité de base de l’informatique quantique représentant
une particule dans un état de superposition. Les états
d’un qubit peuvent être représentés dans
la sphère de Bloch, qui comporte trois axes : X, Y et Z.
Les pôles de la sphère, alignés sur l’axe
Z, représentent les états
. C’est le phénomène
de superposition. Par analogie avec l’informatique classique, nous appelons
qubit l’unité de base de l’informatique quantique représentant
une particule dans un état de superposition. Les états
d’un qubit peuvent être représentés dans
la sphère de Bloch, qui comporte trois axes : X, Y et Z.
Les pôles de la sphère, alignés sur l’axe
Z, représentent les états 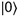 et
et 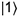 .
.L’état d’un qubit peut être manipulé à l’aide de portes quantiques, qui peuvent être représentées par des rotations dans la sphère de Bloch : les portes de Pauli, qui consistent en des rotations de 180° autour des axes X, Y et Z, et la porte d’Hadamard, qui consiste en une rotation de 90° autour de l’axe Y.
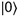 ou
ou 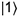 . Cette évaluation
soulève des problèmes d’interprétation,
notamment à propos de l’état quantique :
préexiste-t-il à la mesure (théorie des
mondes multiples d’Everett) ou est-il engendré par la mesure
elle-même (interprétation de Copenhague ?
Il faut noter également que la mesure altère définitivement l’état
du qubit.
. Cette évaluation
soulève des problèmes d’interprétation,
notamment à propos de l’état quantique :
préexiste-t-il à la mesure (théorie des
mondes multiples d’Everett) ou est-il engendré par la mesure
elle-même (interprétation de Copenhague ?
Il faut noter également que la mesure altère définitivement l’état
du qubit.Le qubit est donc une variable stochastique : nous ne pouvons déterminer sa valeur que de manière statistique (par une répétition des mesures), mais il est impossible de connaître sa valeur à un moment précis. Un peu comme nous pouvons estimer les chances qu’il pleuve ou qu’il fasse beau, sans pouvoir affirmer que la pluie ou le soleil sera là avec certitude.
À bien des égards, le qubit évoque les bits probabilistes, également appelés p-bits, dont la valeur fluctue entre 0 et 1. Des travaux de recherche démontrent la possibilité d’émuler certains circuits quantiques au moyen de p-bits. Cela concerne principalement les algorithmes d’optimisation quantique, dont l’objectif est de trouver le maximum ou le minimum d’une variable donnée, comme le temps de trajet. L’avantage est que, contrairement aux qubits, les p-bits peuvent être utilisés à température ambiante ou presque, et ils sont moins sensibles aux erreurs de mesure.
3. Intrication
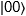 ,
, 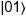 ,
, 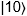 ou
ou 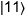 , où le
premier chiffre représente l’état du premier qubit et
le deuxième chiffre représente l’état
du deuxième qubit. Pour manipuler l’état de deux
qubits, il existe des portes quantiques qui peuvent être
déduites des portes à un qubit et du produit de
Kronecker. La porte à deux qubits la plus connue est la
porte CNOT, équivalente à une condition. L’état
du qubit cible est inversé si le qubit de contrôle
est égal à 1. La porte CNOT est utilisée
dans la génération des états de Bell.
, où le
premier chiffre représente l’état du premier qubit et
le deuxième chiffre représente l’état
du deuxième qubit. Pour manipuler l’état de deux
qubits, il existe des portes quantiques qui peuvent être
déduites des portes à un qubit et du produit de
Kronecker. La porte à deux qubits la plus connue est la
porte CNOT, équivalente à une condition. L’état
du qubit cible est inversé si le qubit de contrôle
est égal à 1. La porte CNOT est utilisée
dans la génération des états de Bell.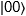 et
et 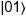 ne sont pas présents, car le premier
qubit ne change pas lorsque le deuxième passe de l’état
ne sont pas présents, car le premier
qubit ne change pas lorsque le deuxième passe de l’état 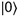 à
à 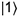 . Soulignons que l’intrication ne dépend
pas de la distance, ce qui permet des interactions quantiques à longue
distance.
. Soulignons que l’intrication ne dépend
pas de la distance, ce qui permet des interactions quantiques à longue
distance.4. Téléportation
La téléportation quantique est un protocole de communication qui repose sur le phénomène d’intrication quantique. Ce protocole permet de transférer l’état d’un qubit sur un autre qubit, quelle que soit la distance qui les sépare.
Contrairement à une idée courante, la téléportation quantique ne consiste pas en un clonage. En réalité, une fois que la téléportation est réalisée, l’état du qubit d’origine devient indéfini. Cela signifie que l’information contenue dans le qubit initial est transférée instantanément, sans que sa copie exacte soit créée.
Un point important à retenir est que la téléportation quantique requiert une transmission classique d’informations pour qu’il soit possible de déterminer l’état du qubit d’origine. Ainsi, afin de reconstituer l’état du qubit initial du côté du destinataire, des informations classiques doivent être transmises en parallèle de la téléportation proprement dite.
Une conséquence...
Quelques conseils avant de démarrer son projet
1. Trouver un cas d’utilisation pertinent
La première étape avant d’appliquer un algorithme quantique est d’identifier un cas d’utilisation pertinent. Par exemple, utiliser l’informatique quantique pour vous aider à choisir votre café ne constitue pas un cas d’utilisation pertinent.
Intuitivement, nous comprenons qu’il y a toute une série de tâches pour lesquelles l’informatique quantique n’offre aucun intérêt par rapport à une approche classique ou tout simplement à une intervention humaine.
Comme vu précédemment, là où l’informatique quantique offre de bonnes perspectives d’application, c’est pour tout ce qui touche aux problèmes d’optimisation et de cryptographie. Aujourd’hui, cependant, les applications de cryptographie basées sur la technologie quantique (utilisant le canal QKD - cf. chapitre Comprendre les tenants et les aboutissants - sous-section Sécurité) en sont à leurs balbutiements. Il n’existe tout simplement pas d’infrastructure accessible au grand public que nous pourrions utiliser pour échanger des clés quantiques. Restent alors les problèmes d’optimisation, que nous pourrions résoudre avec des plateformes cloud telles qu’IBM Quantum.
Le jeu Tetris, par exemple, pourrait constituer un bon problème d’optimisation pour l’informatique quantique : il faut, à un moment donné, trouver la combinaison qui minimise la taille de la pile, ainsi que le nombre d’espaces entre les briques. Bon nombre de jeux de stratégie sont également des problèmes d’optimisation : il faut minimiser ou maximiser des ressources tout en considérant plusieurs combinaisons possibles. Citons les échecs, le go, le poker, ou encore Age of Empires ou StarCraft. En revanche, bien qu’il s’agisse là d’un problème d’optimisation, trouver la note la plus basse dans un groupe de dix élèves est une tâche à la portée de n’importe quelle personne ou de n’importe quel algorithme classique. Un bon problème d’optimisation pour l’informatique quantique est donc un problème difficile à résoudre pour une personne ou pour une machine conventionnelle. En fait, un problème d’optimisation où une approche classique, surtout avancée, n’arrive pas à délivrer de bons résultats est un cas d’étude parfait pour l’informatique quantique.
En ce qui concerne le domaine d’application, il ne reste plus qu’à être imaginatif : de l’analyse des signaux au traitement du langage naturel, en passant par les jeux vidéo, il y a énormément de problèmes qui sont des problèmes d’optimisation (cf. chapitre Comprendre les tenants et les aboutissants - sous-section Trouver des domaines d’application).
2. Approche générale pour l’optimisation quantique
Afin de décrire l’approche générale, nous allons nous intéresser au problème suivant : « Comment améliorer le contraste d’une application web ? »
Certes, pour le résoudre, nous pourrions demander l’avis d’un designer ou recourir à un framework tel que Material UI ou IBM Carbon Design System. Cependant, il va nous permettre d’illustrer la démarche simplement.
a. Transformer son problème en problème d’optimisation
La première étape consiste à formuler notre problème sous la forme d’un problème d’optimisation. « Comment améliorer le contraste d’une application web ? » peut être reformulé ainsi : « Parmi un ensemble de couleurs de texte et de fond, comment trouver une combinaison qui maximise le contraste d’une application web ? » Il s’agit de réécrire le problème de sorte que l’objectif soit désormais de trouver une variable (ici, la couleur de texte et de fond) qui optimise (ici, maximise) le résultat d’un calcul (ici, le contraste).
Cette nouvelle formulation présuppose qu’il existe :
-
un ensemble de couleurs de texte possibles (noir et blanc, par exemple) ;
-
un ensemble de couleurs de fond possibles (orange et bleu, par exemple) ;
-
une formule pour mesurer le contraste d’un texte sur un fond. Nous pouvons calculer la luminance relative, par exemple. Il s’agit du rapport d’intensité entre deux couleurs, le noir étant la couleur la moins intense, et le blanc la couleur la plus intense. Cette luminance relative est comprise entre 1 (noir sur noir) et 21 (blanc sur noir).
Écrivons un pseudo-algorithme qui résout ce problème :
Commençons par définir nos variables.
// Nos couleurs de texte
COULEURS_TEXTE = Noir, Blanc
// Nos couleurs de fond
COULEURS_FOND = Orange, Bleu
// La meilleure combinaison de couleurs
// (par défaut les premières couleurs dans chaque ensemble)
MEILLEUR_COUPLE_COULEURS = {Texte=Noir ; Fond=Orange}
// Le contraste maximum
CONTRASTE_MAXIMUM = luminance relative de Noir et Orange Calculons ensuite le contraste pour chaque combinaison de couleurs de texte et de fond. Si, pour une combinaison, le contraste maximum calculé est supérieur au contraste maximum courant, nous mettons à jour le contraste maximum et le meilleur couple de couleurs.
Pour chaque couleur de texte T dans COULEURS_TEXTE :
Pour chaque couleur de fond F dans COULEURS_FOND :
CONTRASTE = luminance relative de T et F
Si CONTRASTE > CONTRASTE_MAXIMUM :
CONTRASTE_MAXIMUM = CONTRASTE
MEILLEUR_COUPLE_COULEURS = {Texte=T ; Fond=F} Une fois toutes les combinaisons testées, nous sommes sûrs que le meilleur couple de couleurs courant est le couple de couleurs avec le plus grand contraste parmi toutes les combinaisons.
Retourner MEILLEUR_COUPLE_COULEURS b. Créer un modèle avec la programmation par contraintes
Il peut être assez compliqué de porter le pseudo-code précédent sur un ordinateur quantique parce que ce code est écrit de façon impérative. Voici quelques questions qui se posent :
-
Comment traduire une variable décimale (CONTRASTE, par exemple) sous la forme de qubits ?
-
Comment transposer la notion de boucle dans un ordinateur quantique ?
-
Quelles opérations quantiques permettent de réaliser une comparaison (par exemple CONTRASTE > CONTRASTE_MAXIMUM) ?
Certains ordinateurs quantiques permettent...
Mot de la fin
À travers ce livre, notre objectif était de vous transmettre les concepts essentiels de l’informatique quantique, de sorte que vous puissiez mesurer son potentiel et comprendre les enjeux de la recherche dans ce domaine.
Notre objectif était également de vous fournir une méthode pour tester et mettre en place l’informatique quantique dans le cadre d’un projet.
Vous avez désormais toutes les cartes en main pour réaliser vos propres essais. L’informatique quantique est un domaine en pleine évolution : nous apprenons tous les jours ! La meilleure façon d’apprendre reste encore la pratique. Nous vous encourageons à mettre en application et à tester les concepts que nous vous avons présentés.
Voici quelques ressources que nous vous conseillons :
-
Le Qiskit Textbook (https://qiskit.org/learn/). C’est la ressource officielle d’IBM et de Qiskit. Vous y trouverez des informations à la fois théoriques et pratiques. Il existe actuellement un effort de la communauté pour traduire cette documentation dans plusieurs langues. Elle sera donc bientôt disponible en français.
-
La Quantum Open Source Foundation (https://qosf.org/). C’est une organisation à but non lucratif qui réunit des compétences transversales (matérielles, logicielles, en physique, etc.). Elle propose des conférences, des financements pour les projets open source, et aussi des programmes de mentorat. La fondation recense également les projets open source sur l’informatique quantique (https://github.com/qosf/awesome-quantum-software).
-
L’excellent blog Musty Thoughts (https://www.mustythoughts.com/), écrit par Michał Stechły, un ingénieur passionné. Il explique avec des termes simples des choses compliquées.
-
Le blog de Olivier Ezratty (https://www.oezratty.net/), auteur et consultant en informatique quantique. Il explique aussi avec des mots simples des choses complexes, de surcroît en français.
-
Enfin, sur la thématique de la sécurité quantique, il existe la ressource officielle (en anglais et un peu ardue) de l’Institut américain pour les standards et la technologie (https://csrc.nist.gov/projects/post-quantum-cryptography).
En dehors des applications pratiques (et parfois assez techniques) que nous avons évoquées, l’informatique quantique a indéniablement un impact sur notre perception du monde (et n’a pas fini d’en avoir).
Par exemple, dans le domaine des sciences sociales, le concept d’intrication est utilisé pour décrire le fait qu’une personne est inextricablement liée à la société dans laquelle elle évolue. Ainsi, elle ne peut être considérée de manière isolée ou individuelle. Cette idée souligne l’interdépendance entre l’individu et la société qui le façonne, et met en lumière l’influence réciproque qu’ils exercent l’un sur l’autre. En explorant cette notion d’intrication, nous avons une meilleure compréhension...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
