Probabilité et inférence paramétrique
Introduction
La probabilité est la branche des mathématiques qui traite de l’aléatoire. Elle offre l’ensemble des outils pour définir par exemple les chances de survenance d’un évènement donné ou calculer ce que l’on peut espérer gagner ou perdre dans un jeu ou de manière générale et pratique mesurer le risque d’une décision prise… Il en va de même en statistique, l’aléatoire est ce qui caractérise les objets (échantillons, variables…) et par conséquent, il est impossible de ne pas admettre que les mesures et résultats qui en découlent ne soient entachés d’incertitude.
Ainsi, dans de nombreuses expériences et procédures statistiques (échantillonnage, rééchantillonnage, estimations, tests d’hypothèses…), il est courant de recourir à la simulation de nombres aléatoires pour refléter l’incertitude qui y est associée. Le degré de représentativité des échantillons et de reproductibilité faible de la plupart des expériences relatives aux phénomènes observés en science fait que l’on ne peut qu’inférer dans la majorité des cas, c’est-à-dire conclure ou décider sur la base d’échantillons...
Simulation
R propose un nombre impressionnant de fonctions et de packages permettant de reproduire des expériences aléatoires ou de simuler des modèles. Ces fonctions sont des implémentations des concepts de probabilité allant de l’analyse combinatoire à la génération de nombres aléatoires relative ou non à une loi usuelle.
1. Probabilité et dénombrement
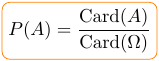
En théorie des probabilités, l’analyse combinatoire offre des méthodes de dénombrement permettant de compter des objets ou éléments relatifs à la réalisation d’un évènement donné sur la base duquel on calcule la probabilité d’occurrence. Ainsi, on a appris que la probabilité de réalisation d’un évènement A donné, est le rapport du nombre de cas favorables à la réalisation de cet évènement au nombre de cas possibles. Formellement, on a :
a. Arrangement
Si l’on considère un ensemble E de n éléments, on parlera d’arrangement de p éléments lorsqu’on prendra tous les cas possibles de p éléments ordonnés dans les n éléments.
Situation avec remise/répétition
En combien de façons peut-on arranger les faces affichées par un dé (à six faces) en trois lancés successifs ?
On est dans un cas dit de p-listes ou p-uplet d’éléments de E = {1,2,3,4,5,6} à cause de l’ordre :
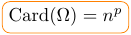
Avec R, il existe une fonction avec laquelle on peut simuler une telle expérience pour ensuite en décompter le nombre d’occurrences. La fonction native qui permet de réaliser ceci est expand.grid() :
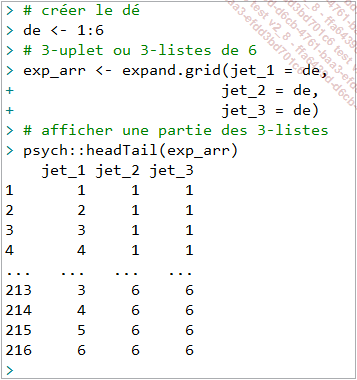
On peut lire grâce au nombre d’éléments affichés qu’il y a exactement 216 cas possibles ce qui est exactement ce qu’on a appris à faire en cours de collège :

Et comme à son habitude R dispose d’un package pour réaliser des expériences de ce type qui peuvent sembler être de simples jeux, mais qui ont de fortes implications en théorie de probabilité. Il s’agit de prob, qui a la fonction rolldie() qui permet de simuler des lancés de dé. Son argument times...
Estimation par intervalle de confiance
Comme on l’a étudié dans les chapitres précédents, plusieurs mesures statistiques sont utilisées pour estimer des caractéristiques relatives à une population donnée. Ces dernières sont appelées alors paramètres. Il peut s’agir de la moyenne, la proportion (un pourcentage), d’une variance… l’idée est de pouvoir sur la base d’un échantillon provenant de la population, estimer le ou les paramètres d’intérêt en recourant aux mesures statistiques de l’échantillon. Outre les aspects de faisabilité d’ordre méthodologique liés à la démarche on a la contrainte de coût qui pousse le statisticien à considérer un échantillon au lieu de la population dans son ensemble.
Pour cela, on distingue l’approche ponctuelle de l’approche par intervalle de confiance pour construire un bon estimateur. Ces deux approches sont plus complémentaires qu’exclusives. En effet, l’approche par intervalle est basée sur le résultat issu de l’approche ponctuelle. Elle consiste à trouver un intervalle plausible dans lequel on est sûr pour un certain niveau de confiance que le paramètre estimé se trouve.
Ainsi, dans cette section on abordera l’approche par intervalle de confiance essentiellement à travers des fonctions R pour les mesures statistiques les plus usuelles.
1. Intervalle de confiance d’une moyenne
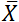 mesurée sur un échantillon
donné change d’un échantillon à l’autre,
donc elle subit des variations, ce qui fait d’elle une variable
aléatoire qui obéit à une certaine distribution
qu’il est utile de connaître dans certains cas.
mesurée sur un échantillon
donné change d’un échantillon à l’autre,
donc elle subit des variations, ce qui fait d’elle une variable
aléatoire qui obéit à une certaine distribution
qu’il est utile de connaître dans certains cas. a. Formulation
On suppose qu’on veut construire un intervalle de confiance de 100(1 - α) % où (α est le risque d’erreur) pour la moyenne inconnue d’une population normalement distribuée. En d’autres termes, il s’agit de trouver un intervalle pour lequel, la probabilité que la vraie moyenne de la population...
Tests d’hypothèses
Une hypothèse au sens statistique du terme est une simple supposition ou affirmation qui peut porter sur l’une des mesures statistiques abordées jusqu’ici à savoir la proportion, la moyenne, etc. Ou sur d’autres statistiques comme le coefficient de la droite de régression ou encore sur l’existence ou non de différence d’un traitement donné sur des groupes d’individus, etc.
En statistique, une supposition ou affirmation est souvent définie comme hypothèse nulle H0, que l’on teste à la lumière des données dont on dispose, car pour chaque hypothèse nulle, il y a toujours une hypothèse alternative H1. Ainsi donc, réaliser un test d’hypothèse c’est utiliser des données pour confirmer ou rejeter une supposition qui fonde ensuite la prise de décision. Par conséquent, les tests d’hypothèses constituent une approche décisionnelle de la statistique inférentielle.
Dans cette section, on va aborder les tests les plus courants à travers les fonctions R.
1. Terminologie
Puisqu’on va procéder à l’étude des tests les plus usuels, on va dans cette section décrire quelques concepts communs à tous les tests et qui seront constamment utilisés dans les explications et qui sont un prérequis à la compréhension des applications qui vont suivre.
a. Formulation d’un test
Comme on l’a dit plus haut, une hypothèse est donc une supposition qui peut être vraie ou fausse, mais qui est a priori admise comme vraie jusqu’à ce que des preuves de sa confirmation ou de son rejet soient apportées sur la base de données collectées (ceci étant une des bases de la méthode scientifique).
Ainsi donc, tester la supposition ou plus formellement réaliser un test d’hypothèse implique de comparer les données collectées à ce qui aurait pu être observé si l’hypothèse nulle était vraie.
-
Hypothèse nulle H0 : c’est une affirmation sur un paramètre donné de la population. Exemple : la proportion des femmes est de 50 % ou la moyenne d’âge de l’échantillon A est égale à celle de l’échantillon...
Méthodes de rééchantillonnage
Il arrive parfois qu’il soit trop complexe d’obtenir une distribution de la statistique d’un test ou tout simple de déterminer avec une méthode traditionnelle un estimateur robuste d’un paramètre surtout lorsqu’on ne dispose que d’un petit échantillon de données.
En statistique moderne, il existe des méthodes dites de rééchantillonnage qui consistent à tirer sur la base d’observations échantillonnées de nouveaux échantillons hypothétiques qui reflètent les caractéristiques de distribution de la population sous-jacente à l’échantillon initial. Ainsi, les applications des méthodes de rééchantillonnage en inférence statistique sont variées. Elles peuvent servir à l’estimation d’intervalles de confiance et à la réalisation de tests d’hypothèses relatives à n’importe quel paramètre.
Les plus connues des méthodes de rééchantillonnage sont notamment la méthode de Boostrap et la méthode Jackknife.
1. Boostrap
a. Démarche
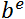 échantillon, on calcule
échantillon, on calcule 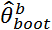 . On peut ensuite déterminer l’estimateur
par Boostrap comme suit :
. On peut ensuite déterminer l’estimateur
par Boostrap comme suit :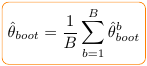
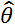 est calculé sur l’ensemble des observations
de l’échantillon d’origine :
est calculé sur l’ensemble des observations
de l’échantillon d’origine :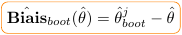
Et l’estimation de la variance par Boostrap est donnée par la relation qui suit :
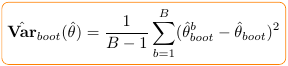
b. Illustration avec le package boot
On peut procéder...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



