L’algorithme k-means
Objectif du chapitre
Les chapitres précédents ont abordé des exemples de deux types d’algorithmes de Machine Learning : les algorithmes de régression et de classification. Ce chapitre porte sur l’algorithme k-means, appelé l’algorithme des k-moyennes en français, qui est un algorithme simple à comprendre et qui fait partie des algorithmes de clustering les plus connus et les plus utilisés.
L’algorithme k-means a été introduit par J. McQueen en 1967. C’est un algorithme non supervisé qui permet de répartir un ensemble de n observations en k clusters. L’objectif après l’application de l’algorithme k-means sur un jeu de données est que chaque cluster contienne des observations homogènes et que deux observations de deux clusters différents soient hétérogènes.
Les domaines d’application de l’algorithme k-means sont nombreux. Par exemple, il est très utilisé pour la segmentation des clients à des fins de marketing, ou encore pour l’isolation des motifs dans les images, car justement les images présentent souvent des régions homogènes, notamment en matière d’intensité lumineuse.
De manière générale, le succès de l’algorithme k-means et de ses versions réside dans sa simplicité...
k-means du point de vue géométrique
Comme précisé au début de ce chapitre, l’algorithme k-means est très intuitif et simple à comprendre. Avant d’entrer dans les détails, il faut noter que k-means, comme tous les algorithmes de clustering, ne nécessite pas l’étiquetage des données, car c’est une procédure non supervisée.
De façon informelle, étant donné n observations à répartir sur kclusters, k-means choisit initialement, de manière aléatoire, k observations parmi les n observations, comme étant les centres des k clusters recherchés. Chacune des n observations sera associée au cluster dont le centre est le plus proche parmi les k centres choisis initialement. Une fois que toutes les observations sont associées à leurs clusters respectifs, le centre de chaque cluster est recalculé en fonction des observations qu’il contient. Puis, de nouveau, chacune des observations est associée au cluster dont le centre est le plus proche de cette observation par rapport à tous les centres des autres clusters. Ces opérations de recalcul des centres des clusters puis d’association des observations aux clusters les plus proches sont répétées jusqu’à ce qu’un critère d’arrêt soit atteint.
L’algorithme k-means utilise une fonction pour calculer les distances entre les observations et les centres des clusters. Ce calcul des distances peut être basé sur la distance euclidienne, la distance de Manhattan ou toute autre fonction permettant de mesurer la dissimilarité entre les observations.
Pour mieux comprendre cet algorithme de clustering, cette section déroule l’algorithme k-means sur un exemple simple. Soit six observations a, b, c, d, e et f à répartir sur deux clusters C1 et C2 ; supposons que la distance utilisée est la distance euclidienne classique. Ces six observations sont définies dans un espace à deux dimensions et leurs coordonnées sont indiquées dans le tableau suivant :
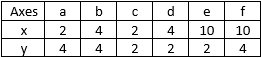
Figure 10-1 : un simple jeu de données avec leurs coordonnées en deux dimensions
Pour rappel, la distance euclidienne entre deux observations A=(xA,yA) et B=(xB,yB) est calculée grâce...
k-means du point de vue algorithmique
L’exemple de la section précédente montre le mécanisme de base de l’algorithme k-means. Les deux paramètres principaux de cet algorithme sont le nombre de clusters k à construire et la fonction utilisée pour le calcul des distances entre les observations. Le schéma général de l’algorithme k-means est présenté ci-dessous :
Entrées : un ensemble d'observations 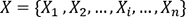 un nombre entier K. correspondant au nombre de
clusters à construire
une fonction de distance
un nombre entier K. correspondant au nombre de
clusters à construire
une fonction de distance 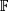 Sortie : une partition
Sortie : une partition 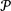 de l'ensemble X en K clusters
1- Initialisation aléatoire des centres
de l'ensemble X en K clusters
1- Initialisation aléatoire des centres 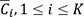 2- Répété :
a) Pour chaque observation Xi, calculer les distances
2- Répété :
a) Pour chaque observation Xi, calculer les distances 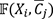 pour tous les j=1..K
b) Association de chaque observation Xi au cluster
dont le centre est le plus proche de Xi
c) Recalculer les centres
pour tous les j=1..K
b) Association de chaque observation Xi au cluster
dont le centre est le plus proche de Xi
c) Recalculer les centres 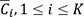 3- Reprendre au point (2) jusqu'à ce que les centres
3- Reprendre au point (2) jusqu'à ce que les centres 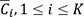 deviennent stables
deviennent stables 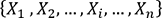 , un paramètre k qui correspond au nombre...
, un paramètre k qui correspond au nombre...Application de k-means avec Scikit-learn
L’application de l’algorithme k-means avec Scikit-learn est très simple et intuitive ! Les exemples ci-dessous montrent comment appliquer cet algorithme sur des jeux de données afin de regrouper les données dans des clusters.
Notez dès à présent que dans les exemples de cette section le nombre de clusters à construire, c’est-à-dire la valeur du paramètre k, est connu à l’avance. Dans la suite de ce chapitre, nous allons voir comment tenter de trouver la valeur optimale de ce paramètre k.
Commençons avec un premier exemple dans lequel nous utilisons les mêmes données que dans l’illustration de la figure 10-2 précédente. Pour réaliser cet exemple, suivez les étapes ci-après.
Créez un nouveau notebook Jupyter, puis saisissez et exécutez les instructions suivantes dans une nouvelle cellule ; vous pouvez également utiliser le notebook k-means-01.ipynb contenu dans le dossier Code de ce chapitre :
%matplotlib inline
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
data = pd.read_csv('../Data/exemple_simple_kmeans-1.csv', sep=',' )
plt.figure(1, figsize=(10, 10))
plt.scatter(data.X, data.Y,s=60)
plt.ylim(0,5) Ces instructions vont tout simplement permettre de charger les modules nécessaires à notre exemple et de lire les données du fichier exemple_simple_kmeans-1.csv. Ces données seront affichées dans un graphique. Remarquez l’import du module KMeans qui sera utilisé pour instancier et utiliser l’algorithme k-means.
L’exécution de ce code affiche un graphique comme celui de la figure ci-dessous :
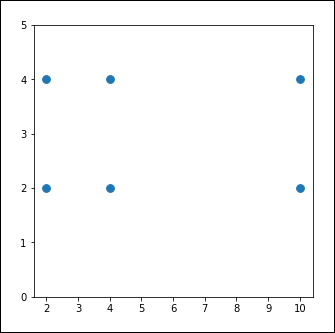
Figure 10-10 : représentation des données en deux dimensions
Dans une nouvelle cellule Jupyter, saisissez et exécutez les deux instructions suivantes :
model = KMeans(n_clusters=2)
model.fit(data) Dans ce dernier code, la variable model permet de créer une instance de l’algorithme k-means....
L’algorithme k-means et les valeurs extrêmes
L’algorithme k-means utilise la notion de distance afin de calculer les centres des clusters recherchés. Bien sûr, la nature de la fonction de calcul de distance utilisée a une influence directe sur les résultats de k-means. Cependant, quelle que soit la fonction de distance utilisée, l’algorithme k-means est sensible aux valeurs extrêmes, comme nous allons le montrer dans l’exemple suivant.
Créez un nouveau notebook, puis saisissez et exécutez le code suivant ; vous pouvez utiliser le notebook k-means-02.ipynb contenu dans le dossier Code de ce chapitre :
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
data = pd.read_csv('../Data/exemple_simple_kmeans-2.csv', sep=',' )
plt.figure(1, figsize=(10, 10))
plt.scatter(data.X, data.Y,s=60)
plt.ylim(0,6)
plt.xlim(0,15) Ce bout de code permet tout simplement la lecture et l’affichage dans un graphique des données du fichier exemple_simple_kmeans-2.csv. Vous obtenez le graphique suivant :
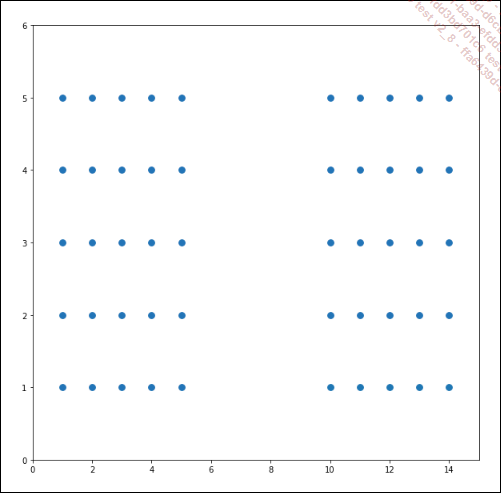
Figure 10-13 : représentation graphique des données définies dans le fichier exemple_simple_kmeans-2.csv
Dans une nouvelle cellule Jupyter, saisissez et exécutez le code suivant :
model = KMeans(n_clusters=2)
model.fit(data)
colormap = np.array(['green','blue'])
plt.figure( figsize=(10, 10))
plt.scatter(data.X, data.Y,c=colormap[model.labels_],s=2) ...Choisir le k de k-means
A priori, lorsque nous sommes face à un grand volume de données sur lequel nous souhaitons appliquer l’algorithme k-means, nous ignorons quel est le nombre de clusters qu’il serait judicieux de construire. On peut imaginer d’exécuter l’algorithme k-means avec plusieurs valeurs du paramètre k et de choisir le partitionnement des données le plus pertinent ! Justement, toute la problématique réside dans la définition de ce qu’est un partitionnement pertinent !
Dans la réalité, l’algorithme k-means est appliqué dans l’un des deux contextes suivants.
|
1. |
Le premier contexte concerne le cas où nous avons une idée, plus ou moins précise, de ce que nous recherchons dans les données. Par exemple, une entreprise de vente de produits électroménagers, tels que les machines à laver ou les lave-vaisselles, utilise k-means afin de réaliser une segmentation de ses clients dans le but de détecter les profils éventuellement intéressés par certaines options de ses appareils. Ici, k-means peut être orienté afin que le clustering soit réalisé autour des options des produits proposés. Pour cela, il suffit de donner plus de poids aux variables décrivant les options de ces produits afin d’indiquer à k-means que les clients qui achètent plus ou moins les mêmes options soient considérés comme faisant partie des mêmes clusters. Dans cet exemple, une fois que k-means est exécuté plusieurs fois, avec à chaque fois une valeur différente du paramètre k, nous pouvons analyser les clusters construits en nous appuyant sur l’idée que les clients d’un même cluster auraient tendance à acheter des produits avec les mêmes options. Si, par exemple, avec une valeur de k égale à 3 les clusters retournés par k-means contiennent des profils très divergents par rapport aux options de leurs produits achetés, alors nous pouvons considérer que la valeur 3 pour le paramètre k n’est pas suffisante pour construire des clusters intéressants ; il serait donc judicieux d’essayer avec des valeurs supérieures à 3 pour ce paramètre... |
Les limites de k-means
Dans cette section, nous allons montrer un exemple où l’algorithme k-means ne réussira pas à répartir les données dans des clusters de façon efficace. Cela va nous permettre de mettre en lumière les faiblesses de cet algorithme. Également, ce nouvel exemple illustrera un cas où les deux métriques Elbow et le coefficient de silhouette ne nous seront pas d’une grande aide !
En effet, comme nous allons le voir, les performances de l’algorithme k-means dépendent directement de l’organisation des données.
Pour la réalisation de ce nouvel exemple, réutilisez votre notebook Jupyter créé lors de l’exemple précédent ou réutilisez le notebook k-means-04.ipynb. Dans les deux cas, la seule modification nécessaire est de remplacer le nom du fichier exemple_simple_kmeans-3.csv par exemple_simple_kmeans-4.csv à partir duquel vous allez lire et utiliser un nouveau jeu de données. Une fois cette modification effectuée, exécutez toutes les cellules de ce notebook afin de pouvoir visualiser les résultats. Ces derniers sont présentés ci-après.
La visualisation de ce nouveau jeu de données est illustrée dans la figure suivante :
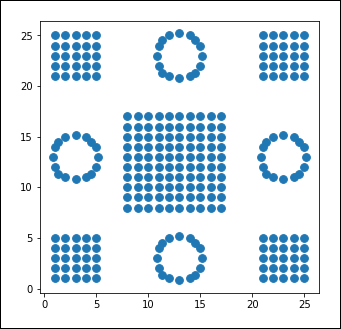
Figure 10-24 : représentation graphique des données du fichier exemple_simple_kmeans-4.csv...
Avantages et inconvénients de l’algorithme k-means
L’algorithme k-means possède bien des avantages, mais aussi des inconvénients. On peut citer les avantages suivants :
-
Il est facile à comprendre et à implémenter.
-
Il implique un temps de calcul acceptable. La complexité de l’algorithme k-means est effectivement de 0(iknm) avec i le nombre d’itérations, k le nombre de clusters, n le nombre d’observations et m la dimension de l’espace de définition des observations.
Parmi les inconvénients majeurs de l’algorithme k-means, on peut citer les points suivants :
-
Le nombre de clusters doit être défini à l’avance.
-
Il converge souvent vers des optimums locaux, en fonction du choix des centres initiaux.
-
Les centres des clusters, mis à part des centres initiaux, sont des objets inexistants puisqu’ils correspondent à des moyennes calculées sur un sous-ensemble d’observations à chaque itération.
-
Une forte influence des valeurs aberrantes sur les résultats.
-
Il donne des résultats médiocres pour les données qui ne sont pas linéairement séparables.
-
Il n’est pas adapté aux données non numériques.
Quelques versions de l’algorithme k-means
Pour pallier les inconvénients de l’algorithme k-means dans sa version classique abordée dans ce chapitre, plusieurs versions ont été développées. Sans entrer dans les détails, on peut citer parmi ces versions :
-
L’algorithme k-medoids : cet algorithme suit le même schéma général que l’algorithme k-means, sauf que k-medoids choisit les centres des clusters parmi les observations déjà présentes. Par rapport à k-means, il présente les deux avantages majeurs suivants :
-
Il est beaucoup moins sensible aux valeurs aberrantes.
-
Les distances entre les observations peuvent être calculées au début de l’algorithme puisque les centres des clusters sont représentés par des observations déjà existantes. C’est un avantage dans la mesure où le nombre d’itérations nécessaires est supérieur au nombre d’observations !
-
-
L’algorithme k-modes : cet algorithme est une adaptation de l’algorithme k-means pour traiter les données de type non numériques. Le centre d’un cluster est calculé en fonction des fréquences des modalités majoritaires présentes dans ce cluster.
-
L’algorithme CLARA : cet algorithme est adapté...
Conclusion
Après avoir présenté le fonctionnement de l’algorithme k-means via des illustrations graphiques, ce chapitre a présenté quelques exemples de code d’utilisation de k-means avec Scikit-learn en portant une attention particulière à la notion de mesure de qualité d’un clustering avec la présentation des deux méthodes Elbow et du coefficient de silhouette. Également, ce chapitre a abordé les limites de l’algorithme k-means via un exemple et évoqué ses avantages et ses inconvénients. Nous avons conclu avec une brève présentation de quelques versions de l’algorithme k-means.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations