La régression linéaire et polynomiale
Objectif du chapitre
Pour résumer, le premier chapitre a permis d’aborder la Data Science de manière théorique ; les deux suivants ont permis d’acquérir une première expérience avec le langage Python et les bibliothèques NumPy et Pandas ; le quatrième chapitre vous a permis de faire vos premiers pas dans l’utilisation de l’environnement Jupyter et le chapitre suivant d’aborder les notions fondamentales des statistiques. Le résultat des courses de ces six premiers chapitres est que vous êtes fin prêt pour attaquer les algorithmes du Machine Learning en commençant par la réalisation de modèles de régression linéaire et polynomiale dans ce présent chapitre.
Le mot « régression » trouve son origine dans une étude publiée par Sir Francis Galton en 1885. Dans cette étude très célèbre, Galton remarque que les pères dont la taille est supérieure à la moyenne ont des fils plus petits qu’eux. A contrario, les pères dont la taille est inférieure à la moyenne ont des fils plus grands qu’eux. De ce constat vient à Galton l’idée de la régression vers la moyenne.
Les algorithmes de régression permettent de faire des prévisions sur des problèmes de natures différentes....
La régression linéaire simple
La régression linéaire simple concerne l’étude de la variation d’une variable à expliquer en fonction d’une et une seule variable explicative. Dans la section La Data Science - Modélisation du problème, nous avons vu que le principe général des algorithmes du Machine Learning supervisés est basé sur l’estimation, à partir d’un échantillon, d’une fonction F qui serait à l’origine des résultats observés. Dans le cas de la régression linéaire simple, ce principe s’applique avec l’hypothèse que la fonction F est linéaire et ne dépend que d’une seule variable.
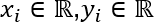 , avec
, avec 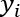 le résultat
correspondant à l’observation
le résultat
correspondant à l’observation 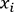 , alors chacun de ces résultats
, alors chacun de ces résultats 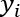 peut être obtenu, du moins approché,
par une fonction
peut être obtenu, du moins approché,
par une fonction 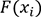 linéaire.
Concrètement, en régression linéaire
simple, la fonction F est supposée égale à
linéaire.
Concrètement, en régression linéaire
simple, la fonction F est supposée égale à  avec
avec 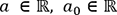 .
.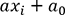 appelée
la droite de régression. Tout le but du jeu est de trouver
des bons estimateurs pour les deux paramètres
appelée
la droite de régression. Tout le but du jeu est de trouver
des bons estimateurs pour les deux paramètres 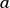 et
et 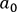 .
.1. La régression linéaire simple de point de vue géométrique
La régression linéaire multiple
La régression linéaire multiple est une généralisation immédiate de la régression linéaire simple. En régression linéaire multiple, la fonction F que l’on souhaite estimer ne dépend plus d’une seule variable, mais de plusieurs.
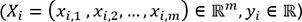 , avec
, avec 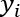 le résultat obtenu pour l’observation
le résultat obtenu pour l’observation 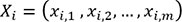 , alors la fonction que l’on souhaite estimer
sera de la forme générale ci-dessous :
, alors la fonction que l’on souhaite estimer
sera de la forme générale ci-dessous :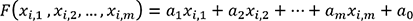
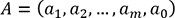 tel que la fonction F soit
la plus proche des
tel que la fonction F soit
la plus proche des 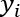 .
.1. La méthode des moindres carrés pour la régression multiple
Tout comme pour la régression linéaire simple, la méthode des moindres carrés peut être utilisée pour la recherche du vecteur A et la fonction à minimiser sera définie comme suit :
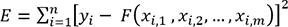 (8)
(8)Les mêmes étapes peuvent être suivies à la différence qu’ici nous allons avoir (m+1) dérivées partielles au lieu de deux. Après un certain calcul, en annulant et en simplifiant ces m dérivées partielles, nous obtenons la solution suivante :
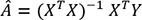 (9)
(9)Avec :
-
l’estimateur du vecteur
-
X la matrice de toutes les observations qui est de la forme :
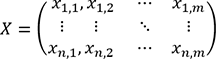
-
XT la matrice transposée de la matrice X
-
Y le vecteur des résultats de toutes les observations de la forme
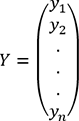
À noter que l’équation (9) suppose que la matrice XTX est inversible.
2. La méthode de la descente de gradient
En plus de la contrainte de la réversibilité de la matrice XTX, l’utilisation de la méthode des moindres carrés peut s’avérer trop consommatrice en temps de calcul lorsque le nombre d’observations n et le nombre de variables m sont très grands.
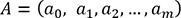 , cet algorithme
suit les étapes ci-dessous :
, cet algorithme
suit les étapes ci-dessous :1: Initialisation aléatoire du vecteur 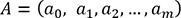 ,
2: Pour chaque
,
2: Pour chaque 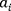 faire
faire
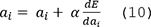 3: Si pas de convergence, reprendre au niveau (2), sinon Fin.
3: Si pas de convergence, reprendre au niveau (2), sinon Fin. La régression polynomiale
La section précédente a montré que la régression linéaire multiple est une généralisation de la régression linéaire simple. Dans le même ordre d’idée, la régression polynomiale est elle-même une généralisation de la régression linéaire multiple. En effet, un modèle de régression polynomiale est un polynôme à plusieurs variables. Par exemple, pour un modèle polynomial d’ordre 2, la fonction F sera définie comme suit :
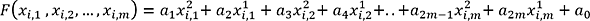
Les modèles polynomiaux permettent de décrire des relations entre les variables qui ne sont pas linéaires. C’est là où réside leur avantage majeur vis-à-vis des modèles de régression linéaire. Cependant, ces modèles nécessitent des temps de calcul plus importants et ils sont sujets au problème de surapprentissage de façon relativement importante.
1. Exemple de régression polynomiale
a. Construction d’un modèle polynomial
Dans ce nouvel exemple, nous allons utiliser le même jeu de données que celui utilisé lorsque nous avons développé des modèles de régression linéaire précédemment dans ce chapitre. Nous allons donc construire des modèles de régression polynomiale pour la prédiction de la pollution de l’air avec l’ozone.
Pour développer notre premier modèle de régression polynomiale, suivez les étapes ci-après.
Commencez par la création d’un nouveau notebook Jupyter. Vous pouvez utiliser le notebook 07-régression_polynomiale.ipynb contenu dans le sous-dossier Code de ce chapitre.
Dans la première cellule de votre notebook, saisissez les instructions suivantes puis exécutez cette cellule afin d’importer les modules nécessaires à la réalisation de votre modèle de régression polynomiale :
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn import preprocessing
from math import sqrt ...Aller plus loin avec les modèles de régression
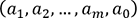 qui donnent des erreurs
qui donnent des erreurs  les moins importantes et qui évitent
le piège du surapprentissage.
les moins importantes et qui évitent
le piège du surapprentissage.Lorsque nous avons abordé la régression linéaire au début de ce chapitre, nous avons vu que la fonction d’erreur à minimiser est la suivante :
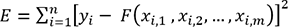
L’approche la plus connue qui permet de minimiser la fonction de calcul d’erreur E tout en évitant le problème de surapprentissage est l’introduction du concept de régularisation.
Il existe deux régularisations très utilisées avec les modèles de régression : la régularisation L1, également appelée régularisation Lasso, et la régularisation L2, ou régularisation Ridge.
1. La régularisation Lasso
Avec la régularisation Lasso (Least Absolute Shrinkage and Selection Operator), la fonction d’erreur à minimiser devient la suivante :
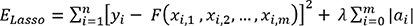
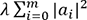 pour sanctionner davantage les solutions avec
des valeurs de
pour sanctionner davantage les solutions avec
des valeurs de 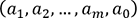 plus grandes.
plus grandes.2. La régularisation Ridge
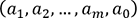 sont davantage sanctionnées...
sont davantage sanctionnées...Conclusion
Ce chapitre a permis d’introduire la régression linéaire et la régression polynomiale. Dans un premier temps, la régression linéaire a été abordée du point de vue géométrique pour donner l’intuition des algorithmes de régression, et dans un second temps la méthode des moindres carrés a été expliquée en détail. Puis des exemples concrets de régression multiple et de régression polynomiale ont été traités avec Scikit-learn. Nous avons profité des exemples réalisés afin d’aborder les notions de normalisation de données, de cross-validation et de surapprentissage et avons aussi détaillé le coefficient de détermination R2. Le chapitre suivant montre comment un algorithme de régression peut être utilisé pour développer un modèle de classification en introduisant la régression logistique.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations