Récursivité

Introduction

Ce chapitre est le second qui introduit la notion de répétition dans les traitements des données après le chapitre « Itération ». Cependant, alors que dans les chapitres précédents, les changements d’états du système s’obtenaient par des instructions qui disaient explicitement les modifications à faire subir aux données, ils s’obtiennent ici en donnant une définition de ces changements. En particulier, les traitements n’utilisent pas l’instruction d’affectation, sauf marginalement, pour donner une valeur à la pseudo-variable Résultat afin de préciser ce que calcule et retourne une fonction.

La deuxième section introduit la récursivité dans les traitements sur les chaînes de caractères. On montre ce qu’est une définition récursive et on applique ce type de définition à la spécification d’algorithmes sur les chaînes de caractères. La section suivante donne quelques exemples de spécifications ou de traitements récursifs sur les nombres. La quatrième section, pour finir, commence l’étude d’un problème que l’on rencontre souvent : l’édition d’un nombre. Il s’agit de transformer un nombre donné pour obtenir les caractères...

Introduction à la récursivité : les chaînes de caractères

La récursivité est introduite dans cette section comme une méthode générale de spécification algorithmique des algorithmes. Cette phrase est déjà, en soi, une phrase qui énonce une propriété récursive : la spécification d’un algorithme est un algorithme.

La première partie présente la récursivité sur un exemple simple : la définition d’un mot du langage. La deuxième partie étudie des exemples de spécifications récursives d’algorithmes de traitement sur les chaînes de caractères. La troisième partie donne la solution complète de quelques exercices instructifs et la dernière, enfin, propose de résoudre divers exercices dont la solution n’est pas développée ici.

Les nombres et la récursivité

Les nombres fournissent de nombreux exemples simples de récursivité. En fait, les définitions mathématiques sont souvent récursives. Cette section vous propose quelques exercices sur ce sujet. Ceux qui ne peuvent se réconcilier avec les Mathématiques peuvent passer à la section suivante.

1. Arithmétique

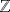Soit l’ensemble des entiers : 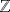= { ..., -2, -1, 0, 1, 2, ...}. On suppose que les seules opérations actuellement définies sur 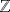sont successeur, qui rend le successeur d’un entier dans la liste ordonnée de ses éléments et prédécesseur la fonction duale de la précédente.

Exercice 6 : Arithmétique sur les entiers

1. Écrire l’algorithme de l’addition de deux entiers.

2. Écrire l’algorithme qui rend l’opposé d’un entier.

La différence de deux entiers est la somme du premier avec l’opposé du deuxième.

3. Écrire l’algorithme qui calcule la différence de deux entiers.

Le produit de deux entiers se calcule en effectuant une addition répétée. Ainsi, par exemple, 7 x 5 est la somme de 5 termes égaux à 7.

4. Écrire les algorithmes de la multiplication et de la division.

Une solution est donnée à cet exercice dans les éléments disponibles en téléchargement...

Nombres et chaînes de caractères : édition d’un entier

On rencontre souvent le problème de l’édition d’un entier dans différents contextes. Cette section aborde ce problème que nous aurons l’occasion de retrouver dans les chapitres ultérieurs et notamment au chapitre « Édition d’un nombre » où son étude sera développée.

En Français, le mot chiffre est utilisé avec plusieurs sens. Il désigne souvent un nombre entier inférieur strictement à la base de numération, par exemple, un nombre entier compris entre 0 et 9 en base dix. Il désigne aussi le caractère représentant l’un de ces nombres, par exemple le caractère ’7’ représentant le nombre 7. Il possède encore bien d’autres sens ; un dictionnaire permet de se rendre compte de la richesse polysémique de ce mot.

Restons en base dix pour simplifier. Nous devons distinguer soigneusement un nombre inférieur strictement à dix du caractère qui représente ce nombre. Il nous faut donc faire une différence bien marquée entre l’objet mathématique, le nombre, qui est indépendant de sa représentation, et le chiffre qui le représente dans un système de codage particulier. Ainsi, le nombre de jours de la semaine est représenté par la chaîne de caractères ’sept’, par le chiffre ’7’, par la suite de chiffres, c’est-à-dire la chaîne de caractères, ’111’ en base deux, etc. Ce que nous devons intégrer, c’est...

Problèmes

Cette section pose quelques problèmes plus difficiles. Ils nécessitent de la réflexion et un peu d’invention pour être résolus d’une façon qui soit praticable ensuite pour être programmée.