Simuler
Introduction
Ce chapitre s’intéresse à des techniques qui permettent de faire des prévisions. Bien que les notions abordées restent élémentaires, le contenu est essentiellement mathématique. Les lecteurs qui n’ont pas le goût de pratiquer ces activités peuvent passer au chapitre suivant.
Il existe des prévisions de nature et de portée différentes. On peut s’intéresser à des événements qui se produiront inévitablement dans l’avenir. C’est le domaine, par exemple, des prévisions météorologiques ou des méthodes de calcul qui cherchent à déterminer le parcours d’un astre sur sa trajectoire. On dispose d’un modèle mathématique qui décrit, plus ou moins bien, la réalité des phénomènes et qui permet de connaître à l’avance, dans une certaine mesure, leur évolution. On peut alors prendre des décisions qui régleront notre comportement. On peut vouloir faire des prévisions sur l’évolution d’un phénomène qu’il est impossible de mettre réellement en œuvre. Comment se comportera la faune de tel cours d’eau en cas de pollution massive par des hydrocarbures ? Quelles sont les conséquences d’un accident d’avion...
Générer des nombres pseudo-aléatoires
Dans cette section, nous étudions la génération de nombres pseudo-aléatoires qui seront ensuite utilisés dans les autres sections. Nous voulons disposer d’une suite de nombres obtenue « au hasard ». Pour l’instant, cette expression signifie que la connaissance de tous les exemplaires des nombres déjà obtenus ne permet pas de déterminer la valeur du prochain nombre à obtenir. Ainsi, par exemple, quand on dispose d’une pièce de monnaie bien équilibrée et que nous l’utilisons pour jouer à « pile ou face », la suite des issues déjà obtenues ne permet pas de connaître le résultat du prochain jet. Tout ce que nous pouvons dire est que ce résultat sera PILE avec la probabilité 0,5 et FACE avec la même probabilité. La suite des issues obtenues est aléatoire.
Préparer un générateur automatique de nombres aléatoires est impossible. Cependant, il existe des techniques de calcul qui permettent d’obtenir des suites qui « imitent » des nombres obtenus « au hasard », au sens défini précédemment. Comme ces générateurs engendrent les nombres à l’aide d’une fonction déterministe, ils sont qualifiés de « pseudo-aléatoires ». La première section étudie quelques exemples simples de générateurs. Cependant, obtenir une suite automatique de nombres ne suffit pas. Il faut disposer de tests qui permettent de s’assurer que les suites obtenues « imitent bien le hasard », autrement dit qu’elles ont les qualités requises pour se substituer aux suites de nombres parfaitement aléatoires. La deuxième section montre comment réaliser quelques tests simples sur de telles suites.
1. Quelques générateurs
Pour générer des nombres « au hasard », on engendre une suite de nombres (xn)n>0 à partir d’un nombre initial donné x0. Une fonction mathématique f permet de calculer xn = f(xn-1). On obtient donc une suite de nombres pseudo-aléatoires puisque la connaissance d’un élément xi quelconque de cette suite permet...
Jeux de hasard
1. Simuler une roulette
Considérons la roulette schématisée par le dessin de la figure ci-dessous.
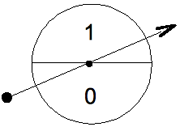
Elle symbolise le fait que les deux issues {0,1} ont la même probabilité 0,5 de sortir. On sait obtenir des nombres aléatoires uniformément répartis sur l’intervalle ]0,1[ depuis la section précédente. Comment obtenir des nombres entiers aléatoires dans {0,1}, chaque issue ayant la même probabilité que toute autre ? Les réels x que nous savons obtenir sont tels que 0 < x < 1. Il suffit donc de sortir 0 pour toute valeur de x entre 0 et 0,5 ou 1 pour toute valeur de x entre 0,5 et 1. La figure ci-dessous schématise ce que nous voulons obtenir.
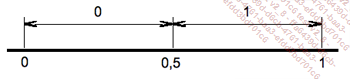
Les nombres générés sont équiprobables. Par conséquent, x appartient à l’intervalle ]0 ; 0,5] avec la probabilité 0,5 et à l’intervalle [0,5 ; 1[ avec la même probabilité. Si on ajoute 0,5 à x, le résultat appartient à l’intervalle ]0,5 ; 1,5[ et la partie entière du résultat vaut 0 ou 1 avec la probabilité 0,5. C’est ce que nous voulons. La figure suivante représente cette situation.

Soit entier la fonction qui retourne la partie entière de son argument. Le principe algorithmique de simulation d’une roulette équitable est donc simple :...
Simulation de processus dynamiques
Cette section étudie deux exemples dont la nature devrait permettre de comprendre en quoi les méthodes des sections qui la suivent sont originales. Ces deux exemples n’apparaissent donc que comme « faire valoir » des sections suivantes. Le premier exemple étudie la propagation d’une rumeur dans une population. Le second montre comment représenter un cas simple de course poursuite.
1. Propagation d’une rumeur
Soit une population humaine homogène de n individus dans laquelle une rumeur se propage de bouche à oreille. On suppose que toute personne ayant connaissance de la rumeur la propage jusqu’à ce qu’elle rencontre une personne qui la connaît déjà. Elle cesse alors de la propager. Nous nous intéressons à l’évolution des effectifs des différentes classes d’individus dans la population. La rumeur s’éteindra, mais atteint-elle tout le monde ? Quel pourcentage de la population reste étranger à cette rumeur ?
Pour réaliser une simulation dynamique de la propagation, on fait des hypothèses sur la fréquence des rencontres de chaque type d’individu. Posons ignore(t) l’effectif de la population qui ignore la rumeur à l’instant t. On note, de même, connaît(t) l’effectif de ceux qui la connaissent mais ne la répandent plus et répand(t) l’effectif de ceux qui la répandent. À tout instant t, on a :
connaît(t) = n - (ignore(t) + répand(t)) Pendant un intervalle de temps (une durée) ∆t, les effectifs ignore(t) et répand(t) évoluent en ignore(t+∆t) et répand(t+∆t). Les contagions se produisent lors de rencontres de type ignore <-> répand qui sont au nombre de ignore(t) x répand(t) et la variation des effectifs correspondants pour un petit ∆t est proportionnelle à ce produit. Nous pouvons donc écrire :
ignore(t+∆t) = ignore(t) - a x ignore(t) x répand(t) Les immunisations se produisent lors de rencontres de type...
Simulation statistique de phénomènes déterministes
Dans cette section, nous proposons des exercices d’écritures d’algorithmes qui montrent comment estimer des résultats parfaitement déterministes en utilisant des nombres pseudo-aléatoires. Nous cherchons donc à obtenir une estimation statistique de résultats qui ne dépendent pas du hasard. Les méthodes mises en œuvre relèvent de méthodes dites de Monte-Carlo en référence à l’univers des jeux de hasard qui ont fait la réputation de la ville du même nom. Ces méthodes sont apparues comme outils de recherche pendant la seconde guerre mondiale afin de simuler le comportement des neutrons dans les matériaux fissiles. Elles sont employées, par exemple, pour calculer des intégrales multiples dites intégrales de configuration.
La section « Calculer π » montre comment calculer une estimation du nombre π. La méthode utilisée est un cas particulier de calcul d’intégrales définies, présenté à la section « Évaluer une intégrale définie ».
1. Calculer π
On donne un disque (D) de rayon r. Nous savons calculer son aire. C’est A(D) = π x r2. Mais combien vaut π ? Cette section montre comment obtenir une...
Simulation de phénomènes aléatoires
1. À la chasse aux mouches
Cette section pourrait s’intituler : le hasard au service d’une névrose !
On veut attraper des mouches pour les enfermer dans un bocal. Les raisons d’un tel comportement ne concernent pas ce livre : dressage, expérimentation scientifique, etc. À chaque capture, il faut ouvrir le couvercle du bocal pour enfermer la nouvelle mouche. Mais alors, chacune des mouches prisonnières, y compris la nouvelle, peut s’échapper, disons avec la probabilité p. Combien de mouches faut-il attraper, en moyenne, pour obtenir un nombre n de prisonnières ? Il s’agit de simuler un certain nombre de telles parties de chasses pour obtenir une estimation statistique du nombre moyen de mouches à attraper pour constituer une collection de n exemplaires.
Il est clair que la simulation, dans la mesure où elle fournit une estimation fiable du résultat attendu, est la seule pratique expérimentale possible. Bien entendu, le problème est suffisamment simple pour être résolu exactement par le calcul, mais ce n’est pas notre propos : nous voulons écrire des algorithmes de simulations.
|
Exercice résolu 3 : Simuler une chasse aux mouches |
Pour simuler une capture, il suffit de faire tourner la roulette à deux issues qui sort l’issue 1 avec la probabilité p et l’issue 0 avec la probabilité (1 - p). La roulette est lancée pour chaque mouche prisonnière afin de déterminer si elle s’échappe ou non. Évidemment, elle s’échappe lorsque la roulette sort 1.
Simuler N chasses pour capturer n mouches au cours de chacune d’elles. Estimer le nombre moyen de mouches à capturer.
Solution
On veut simuler la capture de n mouches. Soit chasse l’algorithme qui simule une partie de chasse. Il doit connaître le nombre n de mouches à capturer et la probabilité p d’évasion d’une mouche capturée. Il retourne le nombre total de mouches capturées pour en obtenir n. C’est donc une fonction dont la spécification est donnée par l’algorithme suivant.
|
Algorithme 7 : Spécification de la fonction chasse |
Algorithme chasse
# Une chasse pour capturer `n' mouches....Notes bibliographiques
Le 147-générateur et le test du poker sont inspirés du petit livre [RAD77] qui propose près de 150 exercices parfois passionnants et dont les solutions sont commentées. Les tests des générateurs sont étudiés d’une façon approfondie par [KNU73b].
Résumé
Ce chapitre a proposé quelques activités simples permettant de simuler des processus déterministes ou aléatoires. Les formules utilisées peuvent paraître parfois impressionnantes, mais le contenu mathématique reste d’un niveau élémentaire. Par contre, les algorithmes proposés sont souvent difficiles à spécifier formellement et les vérifications et les tests des programmes sont d’autant plus difficiles que les résultats sont imprévisibles. Tous les problèmes posés se résolvent aisément par le calcul et il est ainsi possible de vérifier la cohérence des résultats produits par les programmes informatiques avec ceux donnés par les calculs mathématiques.
Bibliographie
[RAD77] Lennart RADE : Tentez votre chance avec votre calculateur programmable ; CEDIC, 1977.
[KNU73b] Donald KNUTH : The Art of Computer Programming - Vol. 2 ; ADDISON WESLEY, 1973.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
