Trier
Introduction
Ce chapitre présente le tri de données comparables. On considère une collection C de données de même type T, quelconque mais COMPARABLE. On veut obtenir une représentation ordonnée des éléments de la collection. Les données seront organisées le plus souvent en tableau. On ne cherche donc pas ici des tris de qualité, évalués selon leurs performances, mais plutôt un prétexte à la construction raisonnée d’algorithmes.
La section « Spécifier un algorithme de tri » commence par poser le problème. C’est la partie difficile du chapitre et elle peut être ignorée en première lecture. En particulier, la spécification algorithmique complète d’un algorithme de tri impose la définition des multi-ensembles invariables et de certaines opérations applicables difficiles à spécifier. La section suivante étudie quelques algorithmes usuellement définis dans une initiation à l’algorithmique. La section « Fusionner deux tableaux triés » montre comment les fusionner pour obtenir un nouveau tableau trié. La section « Exercices », enfin, propose des exercices plus difficiles.
Spécifier un algorithme de tri
Cette section est faite de deux parties. La première présente le problème du tri de données comparables. La seconde étudie la postcondition d’un tri. C’est la partie vraiment difficile du chapitre et elle peut être ignorée en première lecture.
1. Présentation du problème du tri
Soit t un tableau dont les composantes sont d’un type T dérivé de COMPARABLE. On veut un algorithme qui replace dans t ses composantes en ordre, par exemple, croissant. La figure suivante représente un tableau d’entiers avant et après le tri.
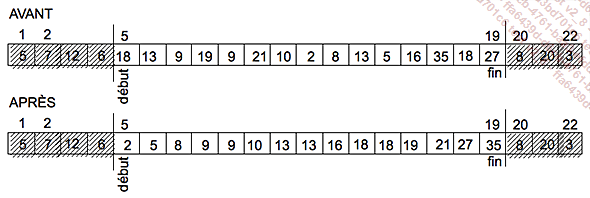
Comme d’habitude, l’algorithme à définir intervient sur une partie précisée du tableau, entre les cases de numéros début et fin. Les données sont replacées en ordre croissant dans le même tableau, qui se trouve donc modifié par l’algorithme. Par conséquent, il s’agit d’écrire une procédure. Les données en entrée sont le tableau t et les numéros des composantes extrêmes début et fin. La signature de la procédure et sa précondition peuvent donc être précisées :
Algorithme tri_ascendant
# Trier `t[début .. fin]' en ordre croissant.
Entrée
t : TABLEAU[T COMPARABLE] # Le tableau à trier
début, fin : ENTIER# Numéros des composantes extrêmes à trier
précondition
# `début' et `fin' sont des index valides de `t'
début ≤ fin => index_valide(t, début) et index_valide(t, fin)
...
COMPARABLE] # Le tableau à trier
début, fin : ENTIER# Numéros des composantes extrêmes à trier
précondition
# `début' et `fin' sont des index valides de `t'
début ≤ fin => index_valide(t, début) et index_valide(t, fin)
...Quelques algorithmes simples
Cette section présente quelques algorithmes simples permettant de trier les éléments d’un tableau. La première partie introduit une stratégie générale naturelle de tri des éléments d’un tableau. De cette stratégie, la seconde partie décline une première solution en étudiant un algorithme qui est aux algorithmes de tri ce que le calcul d’une factorielle est à l’étude de la récursivité : un exercice obligé. Du strict point de vue informatique, les performances d’un tel algorithme sont si pauvres qu’aucun informaticien sérieux n’a songé, un seul instant, à l’utiliser en situation réelle pour trier un volume important de données. Il ne continue à être étudié que pour ses qualités pédagogiques. La troisième partie étudie une seconde solution. C’est un algorithme de tri par permutations qui effectue un peu moins d’opérations que le précédent. Ici encore, ce sont les raisonnements mis en œuvre qui justifient l’étude de cet algorithme. La dernière partie présente quelques variantes du tri par permutations.
1. Tri par permutations : introduction
Soit t un tableau de composantes de type T qui dérive de COMPARABLE. On veut le trier en ordre croissant. Cette opération consiste à amener les grandes valeurs vers le « haut » du tableau, vers la case de numéro fin. En fait, t[fin] contiendra la composante de t[début .. fin] de plus grande valeur. Une stratégie de tri consiste donc à amener la valeur maximum de t[début .. fin] en t[fin] où elle aura alors rejoint sa place définitive. La plus grande valeur de t[début .. fin-1] sera ensuite déplacée en t[fin-1] qui sera sa position définitive... Ainsi, à chaque étape du calcul, le tableau est partitionné en deux sous-tableaux : la partie « haute », qui contient les plus grands éléments et qui n’évoluera plus ; la partie « basse » qui n’est pas encore triée. Considérons, par exemple, la situation représentée par la figure ci-dessous.

La partie...
Fusionner deux tableaux triés
On donne deux tableaux, t1 et t2 triés en ordre croissant. On veut obtenir un tableau Résultat de même type, trié en ordre croissant, qui regroupe les éléments de t1 et t2. La figure ci-dessous illustre l’effet de l’algorithme à étudier.
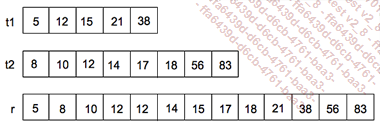
Remarquez que les deux tableaux n’ont pas nécessairement le même nombre d’éléments. Le tableau résultat aura un nombre de composantes égal à la somme des nombres des composantes de t1 et t2. Les éléments identiques dans les deux tableaux sont répétés dans le tableau résultat. D’ailleurs, un même tableau peut contenir des éléments en plusieurs exemplaires.
Si on fusionne t1 entre les cases début1 et fin1 avec t2 entre les cases début2 et fin2, on obtient un tableau résultat qui aura fin1 - début1 + 1 + fin2 - début2 + 1 composantes. Afin de résoudre ce problème facilement, la section suivante commence par introduire un nouveau type de données : le vecteur. C’est un tableau sur lequel sont définies des opérations applicables particulières. La section qui la suivra permettra alors de résoudre le problème de la fusion de deux vecteurs.
1. Définition d’un vecteur
Un vecteur est un sous-tableau d’un tableau simple défini par deux indices début et fin. Des opérations applicables à un vecteur sont aussi définies pour simplifier les algorithmes qui utilisent ces structures de données.
Un vecteur est défini par :
type
VECTEUR
structure
t : TABLEAU[T] # Données associées au vecteur
début : ENTIER# Première case du vecteur dans t
fin : ENTIER# Dernière case du vecteur dans t
invariant
début ≤ fin
index_valide(t, début)
index_valide(t, fin)
fin VECTEUR Un vecteur est déclaré comme un tableau, en précisant le type T des données qu’il contient et les numéros des cases extrêmes, comme ceci :
...
variable
v : VECTEUR[ENTIER][-15, 30]
... Cette « instruction » déclare un vecteur v d’entiers, dont les cases seront numérotées de début = -15 à fin = 30. Pour utiliser un vecteur, il doit évidemment avoir été initialisé. Cette initialisation consiste à donner une valeur à début et à fin, puis à remplir le tableau v.t de données dans les cases dont les indices sont entre début et fin. Cette initialisation étant réalisée, le prédicat est_défini appliqué au vecteur retourne VRAI et les opérations définies dans les paragraphes qui suivent deviennent utilisables.
Il faut bien comprendre ce qu’un vecteur apporte de plus qu’un tableau. Un même tableau permet de définir autant de vecteurs que l’on veut, avec des domaines d’indices qui peuvent éventuellement se recouvrir partiellement. De plus, seules les opérations applicables permettent d’accéder au vecteur et à ses composantes. Ainsi, t, début et fin, par exemple, ne sont pas accessibles pour les clients logiciels du vecteur. Enfin, l’invariant de type étant précisé dans la définition du vecteur, les spécifications des algorithmes qui utilisent les vecteurs s’en trouvent considérablement simplifiées. La suite de cette section va préciser tout cela.
Les opérations applicables à un vecteur se répartissent en trois classes :
-
Les opérations qui permettent de savoir si un indice repère la position d’une composante du vecteur :
-
est_avant (respectivement est_après) est un prédicat qui rend VRAI si et seulement si la position repérée est placée avant la première case (respectivement après la dernière case).
-
est_premier (respectivement est_dernier) rend VRAI si et seulement si la position repérée est celle de la première case (respectivement celle de la dernière case).
-
Les opérations qui permettent d’accéder à la donnée contenue dans la case repérée par la position :
-
item rend une copie de la donnée dans la case repérée ; la donnée accédée n’est pas modifiée.
-
ranger est une procédure qui place une donnée précisée en paramètre dans la case repérée par le paramètre position. La donnée contenue dans cette case avant l’écriture est perdue.
-
Les opérations permettant de déterminer la position repérée :
-
premier (respectivement dernier) retourne le numéro de la première case (respectivement de la dernière case) ; premier(v) retourne donc début et dernier(v) retourne fin.
-
La requête cardinal rend le nombre de composantes du vecteur.
Il s’agit, à présent, de définir ces opérations.
a. Définition des prédicats
Le prédicat est_avant rend VRAI si le paramètre d’entrée position repère une composante avant la première case du vecteur. C’est le cas lorsque position ≤ début - 1. La définition du prédicat est donc :
|
Algorithme 17 : Spécification du prédicat est_avant |
Algorithme est_avant
# `position' repère-t-il avant la première case du vecteur ?
Entrée
v : VECTEUR[T]
position : ENTIER
Résultat : BOOLÉEN
précondition
est_défini(v)
postcondition
Résultat = (position < premier(v))
fin est_avant Remarquez que nous ne pouvons pas définir ce prédicat ainsi dans la postcondition :
...
# INCORRECT !!!
postcondition
Résultat = (position < v.début)
... En effet, les données internes à la structure sont supposées privées et, par conséquent, la valeur de début ne peut pas être accédée dans la postcondition autrement que par les opérations applicables au vecteur.
La fonction est_après est le prédicat dual du précédent et il se définit de la même façon. Ses spécifications sont laissées en exercice. De même, est_premier rend VRAI si et seulement si le paramètre d’entrée position repère la première case, c’est-à-dire si et seulement si position =premier(v).
Le prédicat est_dernier s’écrit de la même façon. Ses spécifications sont laissées en exercice.
b. Primitives de placement dans le vecteur
La fonction premier retourne l’indice de la première case du vecteur :
|
Algorithme 18 : Spécification de la fonction premier |
Algorithme premier
# L'indice de la première case de `v'.
Entrée
v : VECTEUR[T]
Résultat : ENTIER
précondition
est_défini(v)
Réalisation
Résultat v.début
postcondition
est_premier(v, Résultat)
fin premier
v.début
postcondition
est_premier(v, Résultat)
fin premier Remarquez que cette fonction étant une opération applicable à un vecteur, elle accède aux données internes à la structure, ici à début. Cependant, début n’étant pas publique, sa valeur n’est pas accessible directement dans la postcondition.
La fonction dernier se définit de la même façon. Elle est laissée en exercice.
c. Accès aux composantes du vecteur
On accède aux composantes en lecture avec item ou en écriture avec ranger. La fonction item rend une copie de la composante repérée par le paramètre d’entrée position. Sa définition est donnée par l’algorithme suivant.
|
Algorithme 19 : Définition de item |
Algorithme item
# La composante de `v' repérée par `position'.
Entrée
v : VECTEUR[T]
position : ENTIER
Résultat : T
précondition
est_défini(v)
premier(v) ≤ position ≤ dernier(v)
réalisation
Résultat v.t[position]
postcondition
Résultat = (la composante de `v' repérée par `position')
fin lire
v.t[position]
postcondition
Résultat = (la composante de `v' repérée par `position')
fin lire La seconde clause de la précondition s’écrit aussi :
précondition
...
non est_avant(v)
non est_après(v) La procédure ranger place, dans la case repérée par le paramètre position, l’élément e précisé en paramètre. Le contenu de la case avant cette opération est perdu. La définition de cette procédure est la suivante :
|
Algorithme 20 : Définition de la procédure ranger |
Algorithme ranger
# Placer `e' dans la case de `v' repérée par `position'.
Entrée
e : T
v : VECTEUR[T]
position : ENTIER
précondition
est_défini(v)
premier(v) ≤ position ≤ dernier(v)
réalisation
v.t[position]  e
postcondition
# `e' est l'élément de `v' d'indice `position'
item(v, position) = e
# les indices de la structure ne sont pas modifiés
premier(v) = premier(ancien(v))
dernier(v) = dernier(ancien(v))
# Les autres cases ne sont pas modifiées
(
e
postcondition
# `e' est l'élément de `v' d'indice `position'
item(v, position) = e
# les indices de la structure ne sont pas modifiés
premier(v) = premier(ancien(v))
dernier(v) = dernier(ancien(v))
# Les autres cases ne sont pas modifiées
(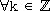 )
(
premier(v) ≤ k < position =>
item(ancien(v), k) = item(v, k)
)
(
)
(
premier(v) ≤ k < position =>
item(ancien(v), k) = item(v, k)
)
(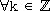 )
(
position < k ≤ dernier(v) =>
item(ancien(v), k) = item(v, k)
)
fin ranger
)
(
position < k ≤ dernier(v) =>
item(ancien(v), k) = item(v, k)
)
fin ranger Il reste à définir l’opération cardinal qui rend le nombre de composantes d’un vecteur. Sa définition ne pose aucune difficulté et elle est laissée en exercice.
Étudions quelques exercices simples pour comprendre comment utiliser ces primitives.
d. Exemples
Exemple 1 :
On donne un vecteur v de nombres réels. On demande de calculer la moyenne arithmétique de ses composantes.
L’algorithme moyenne prend en entrée un vecteur défini de nombres réels et retourne la moyenne arithmétique de ses composantes. Les spécifications sont données par l’algorithme ci-dessous qui traduit directement la définition d’une moyenne.
|
Algorithme 21 : Définition de la moyenne arithmétique d’un vecteur de réels |
Algorithme moyenne
# La moyenne arithmétique des composantes de `v'.
Entrée
v : VECTEUR[RÉEL]
Résultat : RÉEL
précondition
est_défini(v)
réalisation
Résultat  somme(v, premier(v), dernier(v)) / RÉEL(cardinal(v))
postcondition
# Résultat est la somme des éléments de `v[a .. b]'
Résultat =
somme(v, premier(v), dernier(v)) / RÉEL(cardinal(v))
fin moyenne
somme(v, premier(v), dernier(v)) / RÉEL(cardinal(v))
postcondition
# Résultat est la somme des éléments de `v[a .. b]'
Résultat =
somme(v, premier(v), dernier(v)) / RÉEL(cardinal(v))
fin moyenne Il existe au moins une composante puisque l’invariant d’un vecteur défini précise que début ≤fin. Par conséquent, le vecteur n’est défini que s’il possède au moins une composante utile et donc cardinal(v) > 0. Dans le cas contraire, la précondition est fausse. Cette remarque permet donc de calculer directement la moyenne, sans se préoccuper du diviseur de la division.
La somme des composantes est déterminée par une fonction somme qui reste à définir. C’est fait par l’algorithme suivant :
|
Algorithme 22 : Définition de la fonction somme |
Algorithme somme
# Somme des composantes de `v' entre les indices `a' et `b'.
Entrée
v : VECTEUR[(T,+)]
a, b : ENTIER
# les positions extrêmes de `v' dont Résultat est la somme
Résultat : T
précondition
est_défini(v)
premier(v) ≤ a ≤ b ≤ dernier(v)
variable
position : ENTIER
initialisation
Résultat  item(v, a)
position
item(v, a)
position  a + 1
réalisation
jusqu'à
position > b
invariant
Résultat = somme(v, a, position - 1)
variant de contrôle
b - position + 1
répéter
Résultat
a + 1
réalisation
jusqu'à
position > b
invariant
Résultat = somme(v, a, position - 1)
variant de contrôle
b - position + 1
répéter
Résultat  Résultat + item(v, position)
assertion
Résultat = somme(v, a, position)
position
Résultat + item(v, position)
assertion
Résultat = somme(v, a, position)
position  position + 1
assertion
Résultat = somme(v, a, position - 1)
fin répéter
postcondition
# Résultat= La somme des éléments de `v[a .. b]'
a = b => Résultat = a
a < b => Résultat = a + somme(v, a+1, b)
fin somme
position + 1
assertion
Résultat = somme(v, a, position - 1)
fin répéter
postcondition
# Résultat= La somme des éléments de `v[a .. b]'
a = b => Résultat = a
a < b => Résultat = a + somme(v, a+1, b)
fin somme 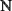 ou T=
ou T=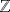 ou…
ou…Exemple 2 :
On veut déterminer la valeur de la composante minimum d’un vecteur. Soit min cette fonction. Sa spécification est la suivante :
|
Algorithme 23 : Spécification de la fonction min |
Algorithme min
# La composante minimum de `vecteur' dans les positions entre
# `a' et `b'.
Entrée
vecteur : VECTEUR[T COMPARABLE]
a, b : ENTIER
Résultat : T
précondition
est_défini(vecteur)
premier(vecteur) ≤ a ≤ b ≤ dernier(vecteur)
postcondition
a = b => Résultat = item(vecteur, a)
a < b => Résultat =
inf(item(vecteur, a), min(vecteur, a+1, b))
fin min
COMPARABLE]
a, b : ENTIER
Résultat : T
précondition
est_défini(vecteur)
premier(vecteur) ≤ a ≤ b ≤ dernier(vecteur)
postcondition
a = b => Résultat = item(vecteur, a)
a < b => Résultat =
inf(item(vecteur, a), min(vecteur, a+1, b))
fin min La fonction inf a déjà été définie au chapitre « Itération ». La spécification de min précise que le résultat est la composante lue dans la case de numéro a si elle est la seule du vecteur. Si elle n’est pas la seule, le résultat est la plus petite des composantes entre celle de numéro a et celle qui est le min du reste du vecteur. C’est donc la même définition, aux notations près, que celle de l’algorithme de même nature étudié au chapitre « Itération ». La fonction inf a été étudiée dans ce même chapitre.
Pour utiliser cette fonction sur tout le vecteur, il suffit de l’appeler avec premier(vecteur) et dernier(vecteur) en paramètres effectifs, comme ceci :
...
# Calcul du minimum du vecteur
minimum  min(vecteur, premier(vecteur), dernier(vecteur))
...
min(vecteur, premier(vecteur), dernier(vecteur))
... La réalisation utilise les opérations définies sur un vecteur. Comme a ≤ b, le domaine d’exploration du vecteur possède au moins une composante. Il suffit donc de le parcourir à partir de cette composante. Le variant de contrôle se déduit simplement de la version étudiée au chapitre « Itération ». Pour l’invariant, il en est de même. On obtient alors la solution suivante, dans laquelle on ne répète pas les spécifications :
|
Algorithme 24 : Réalisation de la fonction min |
Algorithme min
# La composante minimum de `vecteur' dans les positions entre
# `a' et `b'.
...
variable
e : T
position : ENTIER
initialisation
Résultat item(vecteur, a)
position
item(vecteur, a)
position  a + 1
réalisation
jusqu'à
position > b
invariant
Résultat = min(vecteur, a, position - 1)
variant de contrôle
b - position + 1
répéter
assertion
Résultat = min(vecteur, a, position - 1)
e
a + 1
réalisation
jusqu'à
position > b
invariant
Résultat = min(vecteur, a, position - 1)
variant de contrôle
b - position + 1
répéter
assertion
Résultat = min(vecteur, a, position - 1)
e  item(vecteur, position)
si
Résultat > e
alors
assertion
Résultat > e => e = min(vecteur, a, position)
Résultat
item(vecteur, position)
si
Résultat > e
alors
assertion
Résultat > e => e = min(vecteur, a, position)
Résultat e
assertion
Résultat = min(vecteur, a, position)
fin si
assertion
Résultat = min(vecteur, a, position)
position
e
assertion
Résultat = min(vecteur, a, position)
fin si
assertion
Résultat = min(vecteur, a, position)
position  position + 1
assertion
Résultat = min(vecteur, a, position - 1)
fin répéter
...
fin min
position + 1
assertion
Résultat = min(vecteur, a, position - 1)
fin répéter
...
fin min L’exercice suivant complète les exercices résolus précédemment.
|
Exercice 2 : Quelques opérations sur les vecteurs |
1. Compléter l’étude des opérations applicables aux vecteurs.
2. Écrire les algorithmes rang_du_min, max et rang_du_max pour les vecteurs.
Une solution complète de cet exercice est développée dans les fichiers proposés en téléchargement depuis la page Informations générales.
2. Fusion de deux vecteurs triés
La fusion des vecteurs procède à la lecture des composantes. Celles d’un vecteur donné sont lues et enregistrées dans le vecteur résultat tant qu’elles restent inférieures à la composante courante de l’autre vecteur. La difficulté vient du fait que les deux vecteurs n’ont pas nécessairement la même taille. Un vecteur étant épuisé, il faut recopier l’autre. Soient v1 et v2 les deux vecteurs à fusionner, et vr le vecteur résultat. Une version compliquée à écrire utilise deux itérations dans les alternants d’une alternative sur la comparaison des composantes courantes de v1 et v2. Cette version est laissée en exercice. La version qui est proposée ici est plus lisible et plus simple à comprendre.
La lecture ne peut se faire que dans une position entre la première et la dernière composante du vecteur. Lorsque cette position désigne une composante avant la première ou après la dernière, la lecture n’est pas définie. Soit item_max, la fonction de lecture d’un vecteur qui rend INFINI lors d’une tentative de lecture en dehors des limites du vecteur. La spécification de cette fonction est donnée par l’algorithme suivant.
|
Algorithme 25 : Spécification de item_max |
Algorithme item_max
# La composante de `v' d'indice `position' ou INFINI pour
# une lecture hors limites.
Entrée
v : VECTEUR[T]
position : ENTIER
Résultat : T
précondition
est_défini(v)
non est_avant(v, position)
postcondition
(INFINI  T) et (
T) et (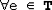 )(e ≤ INFINI)
non est_après(v, position) => Résultat = item(v, position)
est_après(v, position) => Résultat = INFINI
fin item_max
)(e ≤ INFINI)
non est_après(v, position) => Résultat = item(v, position)
est_après(v, position) => Résultat = INFINI
fin item_max La constante INFINI est de type T. Elle est telle que tout élément de T est inférieur ou égal à INFINI.
Ainsi, on peut donc toujours avancer la position et lire dans un vecteur. Pour fusionner les deux vecteurs v1 et v2, on les parcourt en appelant item_max sur celui dont les valeurs des composantes lues restent inférieures aux valeurs des composantes de l’autre vecteur.
La spécification de l’algorithme de fusion est étudiée dans la section suivante.
a. Spécification de l’algorithme de fusion
L’algorithme reçoit, en entrée, les deux vecteurs à fusionner. Il calcule le vecteur résultat vr qu’il retourne en paramètre de sortie. On suppose que le vecteur résultat est défini par l’algorithme qui appelle les services de l’algorithme de fusion. Nous pouvons donc préciser la signature de cette procédure.
|
Algorithme 26 : Signature de fusionner |
Algorithme fusionner
# Fusionner `v1' et `v2' dans `vr' en ordre croissant.
Entrée
v1, v2, vr : VECTEUR[T → COMPARABLE]
... La précondition énonce d’abord les contraintes habituelles sur les vecteurs. De plus, les deux vecteurs en entrée sont triés en ordre croissant et le nombre de composantes déclarées pour le résultat est au moins la somme des nombres de composantes de chacun des vecteurs à fusionner. La précondition s’écrit alors :
...
précondition
est_défini(v1) ; est_défini(v2) ; est_défini(vr)
est_trié_en_ordre_ascendant(v1)
est_trié_en_ordre_ascendant(v2)
cardinal(vr) ≥ cardinal(v1) + cardinal(v2)
... La postcondition exprime que vr est trié en ordre croissant. Les vecteurs v1 et v2 ne sont pas modifiés. Par contre, on doit dire explicitement que tous les éléments des vecteurs en entrée se retrouvent, sans exception, dans le vecteur résultat. Autrement dit, indépendamment de l’ordre des éléments dans vr, le tableau vr.t est la réunion, au sens de la réunion des multi-ensembles, de v1.t et v2.t. La postcondition est alors la suivante :
...
postcondition
est_trié_en_ordre_ascendant
(
vr,
premier(vr),
premier(vr) + cardinal(v1) + cardinal(v2) - 1
)
est_égal_à
(
vr,
premier(vr),
premier(vr) + cardinal(v1) + cardinal(v2) - 1,
union
(
v1, premier(v1), dernier(v1),
v2, premier(v2), dernier(v2)
), premier(v1), dernier(v2)
)
v1 = ancien(v1)
v2 = ancien(v2)
... En toute rigueur, il faudrait redéfinir est_trié_en_ordre_ascendant, union et est_égal_à pour les rendre applicables aux vecteurs. Comme ces redéfinitions consistent à exprimer qu’elles retournent les résultats calculés par leurs homonymes définies sur les tableaux v.t, ce travail ne pose aucune difficulté et est laissé en exercice.
Cette postcondition exprime donc que le résultat vr est trié en ordre croissant dans le domaine des indices entre premier(vr) et premier(vr)-1 augmenté des nombres d’éléments des deux vecteurs fusionnés. De plus, ce résultat est la réunion des deux vecteurs qui ne sont pas modifiés par l’opération.
Nous pouvons passer à l’étude de la fusion.
b. Analyse de la fusion
On lit deux valeurs, V1 depuis v1 et V2 depuis v2 à la position indiquée par la valeur de position jusqu’à ce que les deux vecteurs soient épuisés. On peut donc poser en hypothèse :
Faire une hypothèse sur l’état actuel
Hypothèse (H) : on a lu deux nouvelles valeurs V1 de v1 et V2 de v2. La dernière valeur enregistrée dans vr l’a été à l’indice position-1.
Voir si c’est fini
C’est fini lorsque les deux lectures ont obtenu INFINI puisqu’alors, les vecteurs sont épuisés :
... ...Exercices
1. Tri par insertion dichotomique
Soit t un tableau d’une seule ligne (vecteur) d’éléments d’un type T qui dérivent de COMPARABLE, à trier en ordre croissant. Chaque élément est inséré à sa place dans le résultat à obtenir en recherchant sa position d’insertion par l’algorithme dichotomie étudié au chapitre « Itération ».
Les tris présentés dans la section « Quelques algorithmes simples » plus haut dans ce chapitre n’ont pas utilisé le secours d’un tableau supplémentaire pour construire le résultat. Ils modifient le tableau à trier pour réordonner ses composantes. Nous étudions ici les deux types de solutions en faisant intervenir la méthode d’insertion par dichotomie.
|
Exercice 4 : Tri par insertion dichotomique |
 COMPARABLE.
COMPARABLE.1. Écrire d’abord les spécifications de l’algorithme qui n’utilise pas le secours d’un autre tableau pour calculer son résultat.
Ainsi, les éléments de t sont « triés en place ». Soigner tout particulièrement le pré et la postcondition ; elles ne sont pas faciles à obtenir mais elles fournissent un...
Notes bibliographiques
L’étude des algorithmes de tri est une étape obligée dans l’apprentissage de la programmation. Tous les livres qui traitent de l’algorithmique et des structures de données abordent le sujet, d’ailleurs avec plus ou moins de bonheur. Le plus souvent, les algorithmes présentés dans les livres sérieux sont accompagnés d’une étude de leur complexité algorithmique, ce qui est une évaluation de leurs performances. La référence sur ce sujet reste [KNUTH73b].
Résumé
Ce chapitre a présenté la construction de quelques algorithmes dans le domaine du tri de données organisées en tableaux. Nous avons d’abord étudié la spécification générale d’un algorithme de tri qui n’utilise pas de tableau supplémentaire pour trier les données. Nous avons ensuite présenté la définition d’une structure VECTEUR, qui permet d’itérer simplement sur les données. Cette structure a été utilisée pour écrire un algorithme de fusion en ordre croissant de deux tableaux triés. Des exercices ont permis d’aller plus loin dans la construction d’algorithmes, en abordant l’ordonnancement de tâches soumises à des contraintes de précédence. L’ambition de ce chapitre n’était pas l’étude du tri des données comme problème général. Toute étude sérieuse, même restreinte à quelques solutions types doit être accompagnée d’une évaluation de la complexité des algorithmes proposés, ce qui n’est pas le cas ici.
Bibliographie
[KNUTH73b] Donald KNUTH : The Art of Computer Programming - Vol 3 : Sorting and Searching ; ADDISON WESLEY, 1973.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
