Réseaux de neurones profonds
Objectifs du chapitre et prérequis
Dans le chapitre précédent, nous avons décrit les étapes pour entraîner un classifieur linéaire. Cependant, comme nous l’avons vu, ce type de classifieur a des performances limitées.
Dans ce chapitre, nous allons introduire les réseaux de neurones profonds. Ces modèles d’apprentissage automatique très performants peuvent être utilisés pour résoudre une grande variété de problèmes traitant des données d’entrée et de sortie numériques.
Après les avoir définis, nous listerons les différentes étapes à appliquer pour les entraîner. Certaines de ces étapes sont similaires à celles que nous avons déjà décrites pour les classifieurs linéaires, nous ne les détaillerons donc pas. D’autres étapes, comme la rétropropagation, les fonctions d’activation, ou la gestion du surapprentissage, sont spécifiques aux réseaux de neurones et seront décrites en détail.
Ces dernières étapes sont également utilisées pour entraîner les réseaux de neurones à convolution, une variante des réseaux de neurones profonds conçue spécialement pour traiter les données d’images et de vidéos en préservant...
Neurone formel
Commençons par décrire le neurone formel, qui constitue la brique de base d’un réseau de neurones.
Nous en donnerons deux interprétations : la première est une généralisation des classifieurs linéaires, la seconde est la modélisation des neurones biologiques.
1. Définition du neurone formel
Dans les réseaux de neurones profonds, ce qu’on appelle un neurone est une opération.
Cette opération prend plusieurs entrées. Ces entrées peuvent être les variables d’entrée du réseau, ou la sortie d’un ou plusieurs autres neurones.
Deux opérations sont réalisées par le neurone à partir de ces variables d’entrée :
-
Nous calculons tout d’abord leur somme pondérée : chaque entrée xi est associée à un poids wi, et nous calculons la somme de chaque entrée multipliée par son poids.
-
Ensuite, le neurone applique une fonction non linéaire, appelée fonction d’activation et généralement notée
, au résultat de cette somme pondérée.
L’opération réalisée par un neurone s’écrit de la manière suivante :
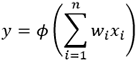
Finalement, la sortie du neurone peut être utilisée comme entrée d’un autre neurone, ou constituer la sortie du réseau.
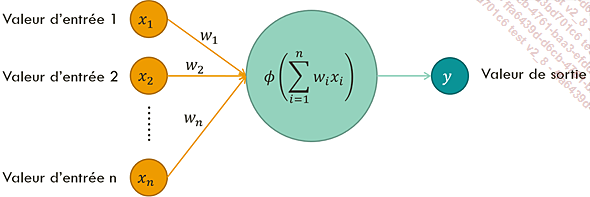
Entrées, opération réalisée et sortie d’un neurone formel
Les valeurs des poids sont estimées pendant l’entraînement.
La fonction d’activation est généralement...
Réseaux de neurones profonds
Nous avons décrit comment fonctionnait un unique neurone formel. Le véritable intérêt de ces neurones apparaît cependant lorsqu’ils sont organisés en réseau.
Nous décrivons dans cette partie la manière dont est organisé un réseau de neurones profond, et quels sont les avantages de ces réseaux.
1. Fonctionnement d’un réseau de neurones profond
Dans un réseau de neurones, les neurones sont organisés en couches. Chaque couche contient plusieurs neurones, et chaque neurone d’une couche est connecté à tous les neurones de la couche suivante.
Les couches autres que la couche d’entrée et la couche de sortie s’appellent des couches cachées. Un réseau avec au moins une couche cachée est un réseau de neurones profond.
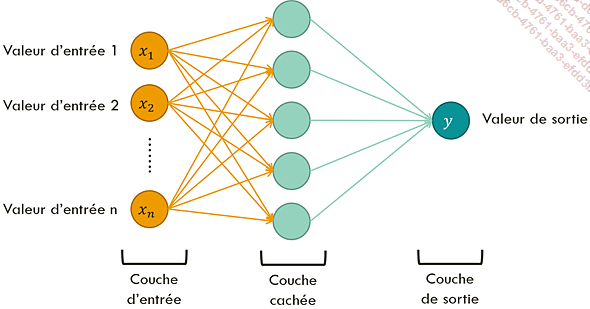
Réseau de neurones profond à une couche cachée, couche qui contient cinq neurones
Lors de la phase de prédiction, les données traversent le réseau de la gauche vers la droite (c’est la propagation avant ou feed-forward propagation en anglais). La prédiction consiste simplement à appliquer les opérations de chaque neurone à toutes les entrées.
Lors de l’entraînement, les informations traversent le réseau de la droite vers la gauche (c’est la rétropropagation, ou backpropagation en anglais), selon un mécanisme que nous détaillerons dans la section Descente de gradient par rétropropagation de...
Étapes de l’apprentissage des réseaux de neurones profonds
Réaliser l’apprentissage d’un réseau de neurones profond (c’est-à-dire estimer les poids optimaux de chaque couche pour une application donnée) se fait en plusieurs étapes.
Tout d’abord, comme lors de l’entraînement d’un modèle linéaire, il est nécessaire de séparer l’ensemble de données en plusieurs sous-ensembles : les données d’entraînement, les données de validation, et les données de test. Cette étape a déjà été décrite en détail dans le chapitre précédent sur les classifieurs linéaires.
Il faut ensuite définir divers hyperparamètres du réseau, comme la fonction d’activation, l’architecture du réseau et divers paramètres de l’optimisation.
Une fois ces étapes terminées, il est possible de passer à l’identification des poids optimaux en utilisant l’optimisation.
Nous allons maintenant détailler chacune de ces étapes une à une.
Optimisation des poids
Chronologiquement, l’optimisation des poids n’intervient pas directement après la séparation des données : il est tout d’abord nécessaire de choisir les hyperparamètres du réseau.
Cependant, la manière dont l’optimisation est faite influence grandement le choix des hyperparamètres, c’est pourquoi nous allons la décrire maintenant.
Nous détaillerons ensuite la manière de sélectionner les hyperparamètres du réseau.
1. Descente de gradient
Il existe plusieurs algorithmes permettant d’identifier les poids optimaux d’un réseau de neurones. Ces algorithmes sont tous des variantes de la descente de gradient.
Nous avons détaillé le fonctionnement de la descente de gradient dans le chapitre précédent : rappelons simplement ici que c’est une méthode d’optimisation relativement simple, permettant de trouver le minimum de n’importe quelle fonction convexe en convergeant progressivement vers celui-ci.
Notons L(w) une fonction multidimensionnelle à minimiser. Dans le cas d’un réseau de neurones, la variable w = (w1, w2,..., wm) est un vecteur représentant l’ensemble des poids du réseau, tandis que la fonction L représente la fonction-coût à minimiser.
Pour chaque élément wi, la mise à jour de l’algorithme de descente de gradient s’écrit de la manière suivante :
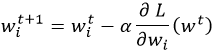
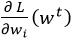 est la dérivée partielle de
la fonction L par rapport à la
variable wi, appliqué en wt.
est la dérivée partielle de
la fonction L par rapport à la
variable wi, appliqué en wt.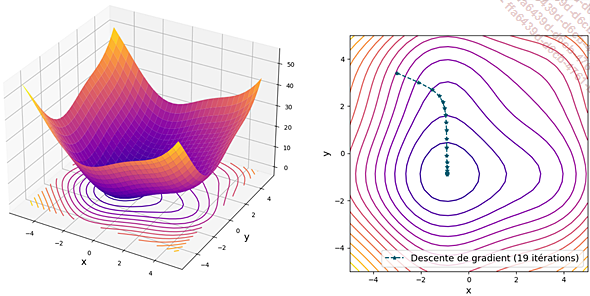
Minimisation d’une fonction convexe à deux variables (à gauche) par descente de gradient (à droite)
Notons que pour un réseau de neurones, la fonction L est rarement convexe ; il n’existe donc aucune garantie que la descente de gradient converge effectivement vers l’optimum global plutôt que vers un optimum local.
C’est cependant cette méthode d’optimisation qui est couramment utilisée, pour deux raisons. Tout d’abord, parce que c’est un algorithme efficace en mémoire et en calculs. Ensuite, parce que des variantes existent qui sont souvent capables de trouver des optima locaux suffisamment bons pour obtenir des résultats satisfaisants...
Fonctions d’activation
1. Caractéristiques des fonctions d’activation
Toutes les fonctions d’activation ont des caractéristiques communes :
-
Elles sont non linéaires ; comme nous l’avons vu dans la section Neurone formel comme la généralisation des classifieurs linéaires, la non-linéarité des fonctions d’activation est une des raisons pour lesquelles les réseaux de neurones profonds peuvent modéliser des fonctions complexes.
-
Elles sont croissantes. Il est important qu’une entrée ayant une grande amplitude se traduise par une sortie ayant une grande amplitude, et inversement pour les entrées ayant une petite amplitude.
-
Ces fonctions et leurs dérivées sont peu coûteuses à calculer : la propagation avant d’un réseau nécessite d’appliquer ces fonctions un grand nombre de fois, et la rétropropagation nécessite un grand nombre de calculs de leur dérivée.
2. Fonctions d’activation courantes
Décrivons maintenant plusieurs fonctions d’activation couramment utilisées.
La fonction sigmoïde est historiquement la première fonction à avoir été utilisée comme fonction d’activation dans un réseau de neurones. Elle est définie de la manière suivante :
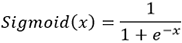
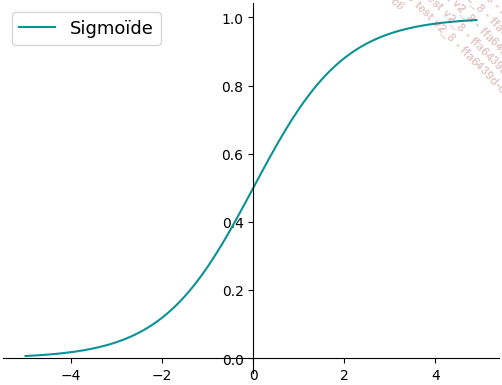
Fonction sigmoïde
Bien qu’elle soit couramment utilisée, cette fonction a plusieurs inconvénients.
Tout d’abord, la présence d’une fonction exponentielle dans sa formulation la rend relativement coûteuse en temps de calcul.
Ensuite, sa forme aplatie aux extrémités...
Surapprentissage
1. Définition
Le but de l’entraînement d’un réseau de neurones profond est de lui apprendre à généraliser à partir d’un ensemble de données.
Cependant, c’est parfois l’inverse qui se produit, et le modèle s’adapte tellement aux données d’entraînement qu’il est incapable de généraliser ce qu’il a appris. Nous parlons alors de surapprentissage (ou overfitting en anglais).
Cela indique généralement que le modèle est trop complexe pour la quantité de données disponible.
À l’inverse, le modèle peut se retrouver en situation de sous-apprentissage (ou underfitting en anglais). Dans ce cas, le modèle n’est pas assez complexe pour capturer la distribution des données.
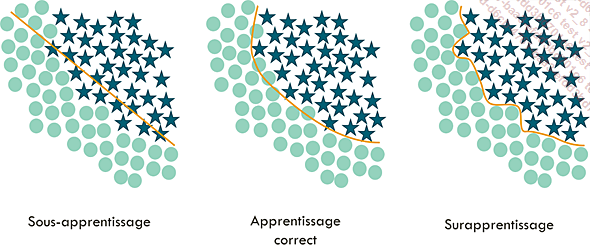
Gauche : sous-apprentissage, avec un modèle linéaire qui est trop simple pour capturer la distribution des données. Centre : apprentissage correct. Droite : surapprentissage, avec un modèle trop complexe, qui se suradapte aux données d’entraînement.
2. Détection du surapprentissage par visualisation de la courbe d’apprentissage
Le surapprentissage et le sous-apprentissage sont facilement visibles dans la courbe d’apprentissage, qui représente la valeur de la fonction-coût en fonction des époques.
En cas de surapprentissage, le modèle se suradapte aux données d’entraînement, aux dépens de ses capacités de généralisation. La fonction-coût est donc beaucoup plus faible sur les données d’entraînement que sur les données de validation.
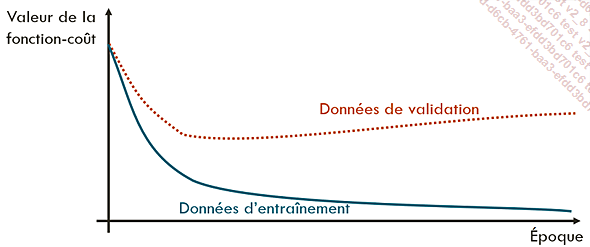
Courbe d’apprentissage en cas de surapprentissage. La fonction-coût est plus faible sur les données d’entraînement que sur les données de validation.
En cas de sous-apprentissage, au contraire, le modèle ne parvient à s’adapter, ni aux données d’entraînement ni aux données de validation. Dans ce cas, la fonction-coût reste très élevée pour les deux ensembles de données, et ne diminue pas, ou très peu, au cours des itérations.
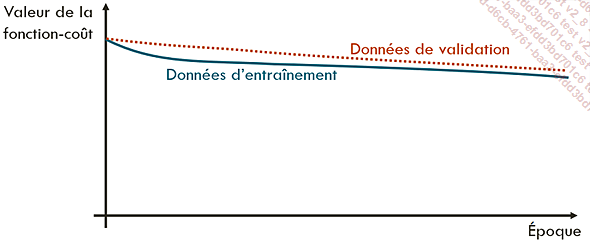
Courbe d’apprentissage en cas de sous-apprentissage. La fonction-coût reste élevée...
Sélection des hyperparamètres
1. Différents types d’hyperparamètres
Un réseau de neurones profond contient plusieurs hyperparamètres, qui ont chacun un impact différent sur les performances du modèle final.
Certains de ces hyperparamètres concernent la structure même du réseau, il s’agit des hyperparamètres suivants :
-
L’architecture du réseau (nombre de couches, nombre de neurones par couche, etc.).
-
Le type de fonction d’activation.
Les autres hyperparamètres concernent la manière dont les poids du réseau sont optimisés, il s’agit des suivants :
-
La taille de lot.
-
La méthode d’optimisation et ses paramètres éventuels.
-
Le taux d’apprentissage utilisé pour l’optimisation.
-
Le taux d’extinction de neurones.
-
Le nombre d’itérations réalisées.
Certains de ces paramètres sont plus critiques que d’autres, et sont généralement fixés en priorité.
2. Ordre et stratégie de sélection des hyperparamètres
La sélection des hyperparamètres est un processus itératif ; il peut être nécessaire de réajuster certains hyperparamètres en fonction des résultats obtenus après l’ajustement d’autres hyperparamètres.
Généralement, nous commençons par ajuster les paramètres les plus critiques pour la performance.
L’hyperparamètre le plus important pour la performance du modèle est l’architecture du réseau.
Le second paramètre le plus important est le taux d’apprentissage.
Ceci peut paraître surprenant ; en effet, nous pouvons penser que, si le taux choisi est trop faible, il suffit de faire plus d’itérations.
En pratique, c’est plus compliqué que cela, pour deux raisons.
Tout d’abord, le taux d’apprentissage n’impacte pas uniquement la vitesse de convergence. Un taux d’apprentissage trop faible peut faire converger le réseau vers un minimum local non désirable (certains mimima locaux présentent des performances correctes, mais ce n’est pas le cas de tous), tandis qu’un taux trop élevé peut ne jamais converger.
Ensuite, la vitesse...
De la création à l’entraînement d’un réseau de neurones profond avec Keras
Nous pouvons maintenant regrouper toutes ces étapes pour créer et entraîner un réseau de neurones permettant de classifier les fleurs d’Iris selon leur espèce.
Ce code se trouve dans le notebook « reseaux_de_neurones_profonds.ipynb ».
Conclusion
Dans ce chapitre, nous avons décrit les neurones formels, et la manière dont ils peuvent être organisés en réseau. Nous avons également détaillé les différentes étapes à réaliser pour entraîner ces réseaux.
Dans le prochain chapitre, nous allons introduire les réseaux de neurones à convolution. Ces réseaux sont une extension des réseaux de neurones profonds, spécialement adaptés au traitement d’images.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



