Editions ENI Livres | Vidéos | e-Formations
Fonction exponentielle et fonctions logarithmes
La fonction exponentielle
Cette fonction, notée exp(x) ou ex, est la seule fonction numérique qui soit identique à sa dérivée et telle que exp(0)=1. Elle admet pour fonction réciproque la fonction logarithme népérien et vérifie la relation exp(x+y)=exp(x)×exp(y).
1. Historique
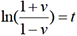équivaut à 
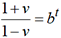, b étant
le nombre tel que ln(b)=1.
Sept ans plus tard, c’est Jean Bernoulli (1667-1748) qui étudie
pour la première fois la fonction exponentielle en tant
que telle. Euler (1707-1783) choisit la lettre e pour représenter la
base des logarithmes népériens et définit
ce nombre par la relation ln(e)=1.Il calcule e avec 23 décimales et démontre que c’est un nombre irrationnel. Charles Hermitte (1822-1901) démontre que e est un nombre transcendant en 1874.
Euler (1707-1783)
2. Définition de la fonction exponentielle par Euler
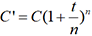. Le problème étudié par
Jacques Bernoulli est le suivant : que devient le nombre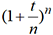 
si n devient
infiniment grand ? En 1748, Euler montre que 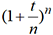tend4 vers et.
Pour t=10% par
exemple,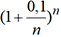 
tend vers 1.1051709180756477...Les logarithmes décimaux
Les logarithmes décimaux (de base 10) ont été inventés par le mathématicien anglais Henry Briggs (1556-1630). Le mot « logarithme » est une contraction des mots grecs « logos » (discours) et « arithmos » (nombre).
1. Historique
Dans l’Europe de la fin du XVIe siècle, les calculs à effectuer étaient longs et volumineux, que ce soit en astronomie, pour le calcul de la position des astres, ou bien dans le secteur financier, pour le calcul des intérêts composés. Il fallait donc les rendre plus faciles et plus rapides.
En 1614, Neper publie Mirifici Logarithmorum Canonis Descriptio, livre dans lequel il explique comment mettre en correspondance les nombres d’une progression géométrique avec ceux d’une progression arithmétique afin que le produit de deux nombres de la progression géométrique corresponde à la somme de leurs correspondants dans la progression arithmétique. La notation abrégée log apparaît en 1616 dans une traduction anglaise de l’œuvre de Neper. Un livre posthume de Neper, publié en 1619, explique comment construire une table de logarithmes. En 1624, Briggs, qui s’inspire des travaux de Neper, publie les premières tables de logarithmes décimaux. Les logarithmes des nombres entiers compris entre 1 et 20 000 y figurent avec 14 décimales. Après Briggs, tous les ouvrages de mathématiques appliquées contiendront une table de logarithmes avec son mode d’emploi. Ces tables de logarithmes resteront d’un usage constant jusque vers la fin des années 1970, époque à laquelle elles seront remplacées par les calculatrices scientifiques.
Henry Briggs (1556-1630)
2. Logarithme décimal d’un...
L’algorithme de Briggs
Publiée en 1624 par Henry Briggs (1556-1630), l’Arithmetica Logarithmica contenait les logarithmes décimaux de 30 000 nombres entiers (de 1 à 20 000 et de 90 001 à 100 000), tous calculés avec 14 décimales.
1. Historique5
Dans l’édition française de 1796 de son Introduction à l’analyse infinitésimale, Euler explique ainsi la méthode utilisée par Briggs pour calculer ses logarithmes décimaux :
« Soit la base logarithmique a=10, qui est celle des tables ordinaires, et proposons-nous de trouver le logarithme approché de 5. Comme ce nombre est renfermé entre les limites 1 et 10, dont les logarithmes sont 0 et 1, on procédera de la manière suivante à l’extraction des racines, et on continuera les opérations jusqu’à ce qu’on soit arrivé à des limites, qui ne diffèrent plus du nombre proposé 5. »
« Ainsi, en prenant des moyennes proportionnelles, on est parvenu à trouver Z=5,000000, à quoi répond le logarithme cherché 0,698970, en supposant la base logarithmique =10. Par conséquent,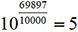 
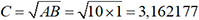à peu près. C’est de cette manière que Briggs et Ulacq ont calculé la table ordinaire des logarithmes, quoiqu’on ait imaginé depuis des méthodes plus expéditives pour les trouver. »
par exemple. Dans la colonne 2, on calcule des
moyennes arithmétiques :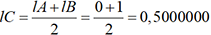 
par exemple. On a ensuite 
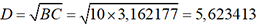et 
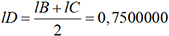puis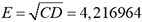 
et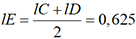 
et ainsi
de suite. Cette démarche revient à trouver des
encadrements de plus en plus fins du nombre log10(5).2. Un programme Python
Le programme qui suit utilise la méthode...
Les logarithmes népériens
Les logarithmes naturels (de base e=2,71828....) ont été inventés au début du XVIIe siècle par le théologien, astronome et mathématicien écossais John Napier ou Neper (1550-1617). C’est Christian Huygens qui montrera le rapport entre les logarithmes naturels et le problème de la « quadrature » de l’hyperbole équilatère. On démontrera plus tard, avec Euler, que la fonction logarithme népérien et la fonction exponentielle sont réciproques l’une de l’autre.
John Napier dit Neper (1550-1617)
1. Historique
Au XVIIe siècle, les mathématiciens européens utilisent la toute nouvelle méthode des coordonnées pour étudier certaines questions de géométrie. On cherche les équations cartésiennes des courbes et de leurs tangentes, on essaye de calculer des aires planes situées entre des courbes et les axes d’un repère par exemple. En 1647, le jésuite flamand Grégoire de Saint-Vincent (1584-1667) tente de résoudre le problème de la quadrature de l’hyperbole. Il démontre que si a, b et c sont des nombres en progression géométrique tous supérieurs à 1, alors les aires comprises entre l’hyperbole, l’axe des x et les droites d’équations respectives x=1 et x=a, x=1 et x=b, x=1 et x=c, sont en progression arithmétique.
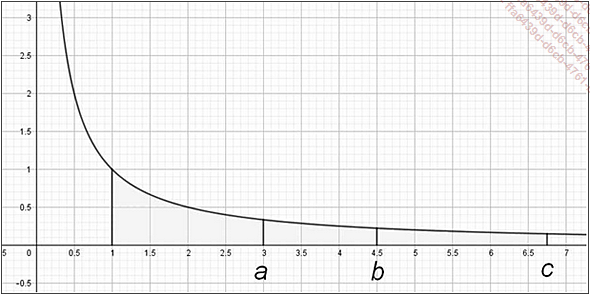
En associant à un nombre positif quelconque a l’aire comprise entre l’hyperbole, l’axe des x et les droites d’équations x=1 et x=a, Grégoire de Saint-Vincent définit ainsi une nouvelle fonction.
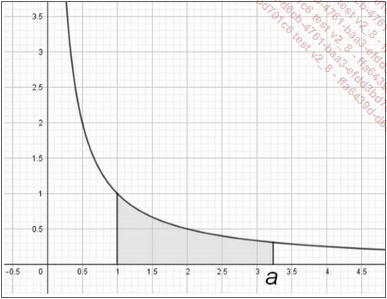
Christian Huygens (1629-1695) montrera ensuite que cette fonction a des propriétés analogues à celles de la fonction logarithme...
