Combinatoire et échantillonnage
Factorielles et combinaisons
 et appelés respectivement factorielle n et combinaison de p parmi n jouent
des rôles importants dans tous les calculs de
probabilités.
et appelés respectivement factorielle n et combinaison de p parmi n jouent
des rôles importants dans tous les calculs de
probabilités.1. Premières recherches
L’analyse combinatoire est une branche des mathématiques qui cherche à dénombrer les éléments d’un ensemble. Cette discipline est issue des préoccupations de grammairiens et de mathématiciens arabo-musulmans. Au VIIIe siècle, al-Khalil Ibn Ahmad (718-791) a essayé de classer tous les mots de la langue arabe. À la fin de ses recherches, il a publié le premier dictionnaire d’arabe, le Kitab al-Ayn. Ces recherches lexicographiques l’ont amené à calculer le nombre total des « mots » de la langue arabe, c’est-à-dire des assemblages de 1, 2, 3, 4 lettres ou plus qui peuvent être formés avec les 28 lettres de l’alphabet arabe.
Tous les assemblages n’ont pas forcément de sens. Autrement dit, il y a moins de mots véritables que d’assemblages de lettres.
2. L’invention des factorielles
Au XIIIe siècle, le mathématicien marocain Ibn Mun’im a publié un livre intitulé La science du calcul dans lequel il a montré comment calculer le nombre des permutations d’un ensemble de n éléments. Ce nombre, noté aujourd’hui n!(factorielle n), est égal à n × (n-1) × (n-2) × ….× 3 × 2 × 1 avec, par convention, 1!=0!=1. Avec Python, les factorielles sont calculées avec l’instruction factorial(n) qui est disponible dans le module math.
# Calcul d'une factorielle
from math import*
n=eval(input("Choisir...Échantillonnage
Soit E un ensemble de n éléments différents et soit p un entier tel que 0 ≤ p ≤ n. Extraire un échantillon de taille p de cet ensemble E, c’est former une partie de E en choisissant au hasard p éléments parmi les n éléments de E.
1. Historique
 , avec
, avec 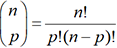 .
.2. Fabrication expérimentale d’un échantillon
Le programme qui suit simule l’extraction d’un échantillon de k boules prises dans une urne qui contient 3 boules rouges, 3 boules bleues et 3 boules vertes. Les boules sont extraites une à une au hasard et sans remise. On peut donner à k n’importe quelle valeur entre 1 et 8. Dans ce programme, les boules rouges sont numérotées de 1 à 3, les boules bleues de 4 à 6 et les boules vertes de 7 à 9.
# Fabrication d'un échantillon de 3 boules
from random import*
indicateur=[]
boulestirées=0
liste=[]
n=9
k=3
# Création de la liste des indicateurs
for i in range(0,15):
indicateur=indicateur+[0]
# Tirage au sort des boules
j=0
while boulestirées!=k:
j=j+1
x=randint(0,n-1)
if indicateur[x]==0:
liste=liste+[x+1]
indicateur[x]=1
boulestirées=...Échantillonnage et fréquences
Si un même caractère est présent dans un ensemble E et dans un échantillon extrait de cet ensemble, on peut se demander quelle est la relation qui existe entre les fréquences de ce caractère dans l’échantillon et dans l’ensemble parent.
1. Fluctuations d’échantillonnage
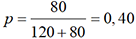 pour les
boules blanches. Pour constituer un échantillon de 40 boules,
on retire une première fois une boule de l’urne, on note
sa couleur, on la remet dans l’urne, on retire une deuxième
fois une boule de l’urne et ainsi de suite. En simulant cette opération, on
a pu établir le tableau ci-dessous qui montre la composition
de 10 échantillons :
pour les
boules blanches. Pour constituer un échantillon de 40 boules,
on retire une première fois une boule de l’urne, on note
sa couleur, on la remet dans l’urne, on retire une deuxième
fois une boule de l’urne et ainsi de suite. En simulant cette opération, on
a pu établir le tableau ci-dessous qui montre la composition
de 10 échantillons :|
Boules blanches |
21 |
18 |
19 |
18 |
11 |
21 |
19 |
15 |
26 |
29 |
|
Boules noires |
19 |
22 |
21 |
22 |
29 |
19 |
21 |
25 |
14 |
11 |
|
Fréquence des boules blanches |
0,525 |
0,45 |
0,475 |
0,45 |
0,275 |
0,325 |
0,475 |
0,375 |
0,35 |
0,275 |
On constate que deux échantillons de même taille issus de la même expérience aléatoire ne sont généralement pas identiques. On appelle fluctuation d’échantillonnage les variations des fréquences constatées.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

