Suites de nombres réels
Suites et racines carrées
L’idée de répéter un calcul en changeant les nombres utilisés à chaque étape est très ancienne puisqu’on en trouve la trace à Babylone, 1800 ans avant J.-C. En Grèce, on a souvent eu recours aux suites pour calculer des racines carrées.
1. La méthode d’Archytas de Tarente
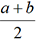 , leur moyenne géométrique g est définie par g2 = ab et leur moyenne harmonique h est définie par
, leur moyenne géométrique g est définie par g2 = ab et leur moyenne harmonique h est définie par 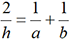 . On démontre que h<g<m. Archytas de Tarente a utilisé cette
relation pour calculer des racines carrées.
. On démontre que h<g<m. Archytas de Tarente a utilisé cette
relation pour calculer des racines carrées.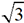 , il commence par écrire
, il commence par écrire 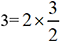 puis, comme le montre le tableau suivant, il
déroule ses calculs :
puis, comme le montre le tableau suivant, il
déroule ses calculs :|
Étape n° |
x |
y |
Moyenne arithmétique de x et de y |
Moyenne harmonique de x et de y |
|
1 |
2 |
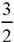 |
 |
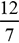 |
|
2 |
 |
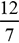 |
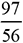 |
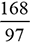 |
|
3 |
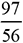 |
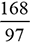 |
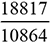 |
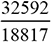 |
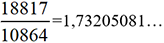 et
et 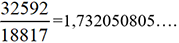 . Le nombre
. Le nombre 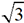 est connu avec une erreur qui porte sur la 9e décimale
seulement. On peut généraliser la méthode
d’Archytas de Tarente à un nombre réel
positif A quelconque en utilisant
le programme qui suit :
est connu avec une erreur qui porte sur la 9e décimale
seulement. On peut généraliser la méthode
d’Archytas de Tarente à un nombre réel
positif A quelconque en utilisant
le programme qui suit :# Calcul d'une racine carrée avec la méthode d'Archytas de Tarente
A=eval(input("Valeur de A : "))
x,y=2,A/2
for i in range(1,6):
m=(x+y)/2
h=x*y/m
print("x=",x," et y=",y)
x,y=m,h On a choisi de faire le calcul en cinq étapes car l’algorithme est très performant. ...
Comment définir une suite ?
À partir du XVIIe siècle, longtemps après les géomètres grecs, de nombreux mathématiciens européens comme Jean Bernoulli ou Newton ont utilisé des suites numériques pour déterminer certaines valeurs numériques ou bien résoudre des équations de manière approchée.
1. Définition
Une suite numérique est une liste de nombres qui sont tous numérotés et rangés dans l’ordre des numéros croissant. En général, on choisit 0 comme rang du premier terme d’une suite (un). Il semble qu’on doive à Joseph-Louis Lagrange (1736-1813) la notation indicielle.
2. Suites définies par un=f(n)
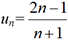 pour n≥ 0. Le calcul donne u0= -1,
pour n≥ 0. Le calcul donne u0= -1, 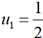 , u2=1,
, u2=1, 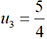 et ainsi de suite. Pour établir la
liste des dix premiers termes de la suite par exemple, on peut utiliser
un programme écrit avec Python :
et ainsi de suite. Pour établir la
liste des dix premiers termes de la suite par exemple, on peut utiliser
un programme écrit avec Python :from math import*
def f(n):
return (2*n-1)/(n+1)
n=eval(input("Choisissez n :"))
for i in range(1,n+1):
print("terme de rang ",i,"=",f(i)) En modifiant ce programme, on peut calculer directement un terme de la suite, le 10 000e par exemple. On obtient un=1.9997000299970003.
from math import*
def f(n):
return (2*n-1)/(n+1)
n=eval(input("Choisissez n :"))
print("Le terme de rang ", n," est ",f(n)) 3. Suites récurrentes
Une suite récurrente (un) du 1er ordre est définie par le choix de son premier terme u1 et par la donnée...
Quand n devient de plus en plus grand
Quelques exemples vont nous permettre de juger de l’intérêt de Python pour observer le comportement des termes d’une suite et faire des conjectures. Les termes sont-ils positifs ? Sont-ils croissants ou décroissants avec n ? Semblent-ils converger vers une limite ? Si oui, peut-on avoir une idée de celle-ci ?
1. Une suite peut être convergente
Dans l’Encyclopédie de d’Alembert et Diderot publiée au XVIIIe siècle, on peut lire la définition suivante :
« Suite : se dit d’un ordre ou d’une progression de quantités qui croissent ou décroissent suivant quelques lois. Lorsque la suite va toujours en s’approchant de plus en plus de quelque quantité finie […] on l’appelle suite convergente et si on la continue à l’infini, elle devient égale à cette quantité. »
Cependant, la notion de limite d’une suite n’a été établie rigoureusement qu’au XIXe siècle par Louis Augustin Cauchy (1789-1857).

Augustin Louis Cauchy (1789-1857)
Exemple 1
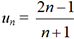 pour n≥ 0. Le programme qui suit
permet de calculer u1000, u10000 ou
même u100000 si
on le veut.
pour n≥ 0. Le programme qui suit
permet de calculer u1000, u10000 ou
même u100000 si
on le veut.n=eval(input("Valeur de n ?"))
u=(2*n-1)/(n+1)
print(" pour n=",n,"u=",u) 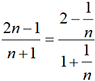 . Cette expression tend vers 2
quand n devient infiniment
grand.
. Cette expression tend vers 2
quand n devient infiniment
grand.Exemple 2
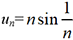 pour n≥ 1. Le programme suivant
permet de calculer les 10 premiers termes de la suite.
pour n≥ 1. Le programme suivant
permet de calculer les 10 premiers termes de la suite.from math import*
n=10
for i in range(1,n+1): ...Une suite célèbre : la suite de Fibonacci
Formé aux mathématiques grecques et arabes, Léonard de Pise dit Fibonacci fut le premier grand mathématicien européen. Il fut très en avance sur son temps et ses ouvrages restèrent ignorés pendant quelques siècles.

Léonard de Pise dit Fibonacci (1180-1250)
1. Historique
Léonard de Pise (1180-1250), plus connu sous le nom de Fibonacci, c’est-à-dire « le fils de Bonacci », est né à Pise, en Italie. En 1202, il a publié le Liber abaci ou livre de l’abaque. Après avoir présenté les chiffres arabes et le système d’écriture décimale positionnelle des entiers utilisés par les mathématiciens arabes, il étudie diverses questions mathématiques : la technique des quatre opérations, le calcul fractionnaire, les calculs commerciaux, les problèmes de change ou de partage, la conversion des monnaies, le calcul des intérêts, etc. On y trouve aussi des problèmes de fausse position, simple ou double, et des problèmes d’arithmétique qui portent sur les nombres parfaits et les nombres premiers.
Dans les deux derniers chapitres sont traitées des questions liées à l’emploi des racines carrées et cubiques ainsi qu’à l’emploi des équations du premier et du second degré, à la manière d’al-Khwarizmi.
2. Le problème des lapins
Le Liber abaci est aussi un recueil de « petits » problèmes dont le plus célèbre est incontestablement celui des lapins :
« Combien de couples de lapins obtiendrons-nous à la fin de l’année si, commençant l’année avec un couple unique de jeunes lapins...
Suites définies par des sommes
Soit (un) une suite de nombre. On définit une nouvelle suite (Sn) en posant S1=u0 S2= u0+ u1+u2, S3= u0+u1+u2+u3 et ainsi de suite. On dit alors que la suite (Sn) est une série numérique de terme général un. Cette série est convergente si et seulement si le nombre Sn a une limite finie quand n tend vers l’infini. L’étude des séries a connu un grand développement à partir du XVIIe siècle.
1. Historique
Les premiers travaux sur les séries sont très anciens. Pour calculer la somme 1+2+3+... + n, les mathématiciens chinois du IIIe siècle après J.-C. utilisaient la figure de l’escalier.
La figure suivante montre le calcul de S=1+2+3+ ..... +10 avec cette méthode.
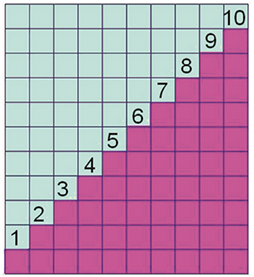
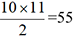 . D’une façon générale,
avec n marches, on obtient
. D’une façon générale,
avec n marches, on obtient 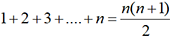 . Le calcul de la somme des n premiers entiers naturels fait
l’objet d’une légende qui concerne le grand mathématicien
allemand Carl Friedrich Gauss (1777-1855). Jeune écolier,
il aurait réussi à calculer la somme des entiers
de 1 à 100 en quelques instants de la façon suivante :
après avoir observé que 1+100=2+99=3+98= ......=50+51,
il aurait annoncé une somme de 5050 en multipliant 101
par 50. L’anecdote est certainement fausse mais la méthode
de calcul est parfaitement exacte et s’applique à n’importe
quel entier n.
. Le calcul de la somme des n premiers entiers naturels fait
l’objet d’une légende qui concerne le grand mathématicien
allemand Carl Friedrich Gauss (1777-1855). Jeune écolier,
il aurait réussi à calculer la somme des entiers
de 1 à 100 en quelques instants de la façon suivante :
après avoir observé que 1+100=2+99=3+98= ......=50+51,
il aurait annoncé une somme de 5050 en multipliant 101
par 50. L’anecdote est certainement fausse mais la méthode
de calcul est parfaitement exacte et s’applique à n’importe
quel entier n.Le programme qui suit calcule la somme S=1+2+3+... n.
# Somme des entiers de 1 à n
n=eval(input("Choisissez l'entier n : "))
S=0
for i in range(1,n+1):
S=S+i ... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

