Géométrie analytique
Équation réduite d’une droite dans le plan
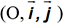 le plus souvent orthonormal, les droites du
plan sont caractérisées par deux types d’équations.
Si k est un nombre réel quelconque,
une perpendiculaire à l’axe des x a
une équation de la forme x=k. Par contre, l’équation
d’une droite qui n’est pas perpendiculaire à l’axe des x est de la forme y=ax+b. Les programmes de géométrie
analytique construits avec Python permettront d’éviter
des calculs assez simples mais vite fastidieux.
le plus souvent orthonormal, les droites du
plan sont caractérisées par deux types d’équations.
Si k est un nombre réel quelconque,
une perpendiculaire à l’axe des x a
une équation de la forme x=k. Par contre, l’équation
d’une droite qui n’est pas perpendiculaire à l’axe des x est de la forme y=ax+b. Les programmes de géométrie
analytique construits avec Python permettront d’éviter
des calculs assez simples mais vite fastidieux.1. Historique
Dans sa Géométrie de 1637, René Descartes (1596-1650) combine le calcul algébrique et les coordonnées pour résoudre des problèmes de géométrie. Il caractérise chaque courbe par une équation de la forme y=f(x) en se limitant toutefois aux seules équations algébriques. Cette restriction l’amène à exclure du champ de ses recherches les courbes du genre y=xsinx, qu’il qualifie de courbes « mécaniques » (aujourd’hui, ces courbes sont dites « transcendantes »).
Descartes applique avec succès sa méthode à la résolution du problème du géomètre grec Pappus d’Alexandrie (IVe siècle après J.-C.) : « déterminer le lieu des points tels que, étant donné quatre droites et étant considéré les distances d’un point à chaque droite sous des angles déterminés, le produit de deux distances est égal au produit des deux autres ». Descartes démontre que ce lieu est une conique. Il démontre également que toute équation du second degré en x et y est celle...
Équation cartésienne d’une droite dans le plan
Vers le milieu du XVIIIe siècle, la géométrie analytique n’a pas encore achevé de définir ses concepts principaux. Dans le plan par exemple, l’axe des x joue toujours un rôle privilégié, ce qui oblige à définir l’équation d’une droite de deux façons différente : soit y=ax+b, soit x=k. La notion d’équation cartésienne va supprimer cette dualité.
1. Historique
Des mots comme « abscisse », « ordonnée » ou « coordonnée » ne seront rigoureusement définis qu’en 1745 dans l’Encyclopédie de Diderot (1713-1784) et d’Alembert (1717-1783). Il faut attendre 1746 pour voir Euler (1707-1783) montrer l’équivalence des deux axes d’un repère du plan et utiliser des changements de repère et de coordonnées. Le plan étant muni d’un repère cartésien, cela permettra à Lagrange (1736-1813) de rétablir cette équivalence en montrant vers 1770 que l’expression ax+by+c=0 caractérise n’importe quelle droite du plan. Cette expression est l’équation cartésienne d’une droite.
2. Recherche de l’équation cartésienne d’une droite dont on connaît deux points
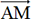 et
et 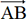 sont colinéaires.
sont colinéaires. 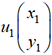 et
et 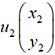 sont colinéaires...
sont colinéaires...Droites dans l’espace
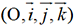 qui peut être orthonormal si on le
désire. L’outil essentiel sera la notion de vecteurs colinéaires.
Toutes les programmes de ces quelques pages utiliseront cet outil.
qui peut être orthonormal si on le
désire. L’outil essentiel sera la notion de vecteurs colinéaires.
Toutes les programmes de ces quelques pages utiliseront cet outil.1. Vecteurs colinéaires dans l’espace
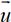 et
et 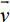 sont colinéaires
si et seulement s’il existe un réel t non
nul tel que
sont colinéaires
si et seulement s’il existe un réel t non
nul tel que 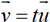 . En d’autres
termes, deux vecteurs colinéaires
. En d’autres
termes, deux vecteurs colinéaires 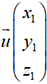 et
et 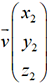 ont des
coordonnées proportionnelles : x2 =tx1y2 = ty1 et z2 = tz1.
ont des
coordonnées proportionnelles : x2 =tx1y2 = ty1 et z2 = tz1.2. Points alignés
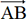 et
et 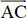 sont colinéaires.
Le programme qui suit permet de vérifier si trois points de
l’espace A, B et C dont les coordonnées sont connues sont
alignés ou non.
sont colinéaires.
Le programme qui suit permet de vérifier si trois points de
l’espace A, B et C dont les coordonnées sont connues sont
alignés ou non.# Les points A, B et C sont-ils alignés ?
from math import*
xA,yA,zA=eval(input("Coordonnées du point A ? "))
xB,yB,zB=eval(input("Coordonnées du point B ? "))
xC,yC,zC=eval(input("coordonnées du point C ? "))
# Calculs et résultats
a,b,c=xB-xA,yB-yA,zB-zA
aa,bb,cc=xC-xA,yC-yA,zC-zA
k1,k2,k3=a*bb-b*aa, b*cc-c*bb,a*cc-c*aa
if k1==0 and k2==0 and k3==0:
print("Les points sont alignés.")
else :
print("Les points ne sont pas alignés.") 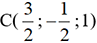 ne le sont pas.
ne le sont pas.3. Représentation paramétrique d’une droite
Équations paramétriques d’un plan
Tout comme les droites, les plans peuvent également être représentés par des équations paramétriques. Aussi, pour démontrer la plupart des résultats qui suivront, on utilisera les mêmes outils que pour les droites, la colinéarité et la résolution de systèmes d’équations linéaires par exemple.
1. Historique
L’application des méthodes de la géométrie analytique à l’espace date du début du XVIIIe siècle. En 1740 par exemple, Alexis Clairaut (1713-1765) propose l’équation (x -xO)2 + (y - yO)2 + (z - zO)2 = r2 pour la sphère de rayon r et de centre O. Un demi-siècle plus tard, Euler (1707-1783) détermine les équations des autres surfaces du second degré puis, vers 1770, Lagrange (1736-1813) établit les équations du plan et systématise l’utilisation des trois axes de coordonnées pour étudier les problèmes de géométrie dans l’espace. Gaspard Monge (1746-1818) étudie de nouvelles surfaces algébriques. Le XIXe siècle voit se développer le calcul vectoriel qui s’ajoute aux outils algébriques dont dispose la géométrie analytique.

Joseph-Louis Lagrange (1736-1813)
2. Détermination de l’équation paramétrique d’un plan
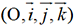 . Soit P un plan défini par la donnée
d’un point A(xA; yA; zA) et de
deux vecteurs
. Soit P un plan défini par la donnée
d’un point A(xA; yA; zA) et de
deux vecteurs 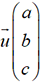 et
et 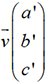 non colinéaires.
non colinéaires.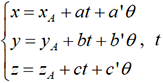 , t et Ө étant
deux nombres réels, constituent une représentation
paramétrique du plan P. Comme un plan est déterminé par
la donnée de 3 points...
, t et Ө étant
deux nombres réels, constituent une représentation
paramétrique du plan P. Comme un plan est déterminé par
la donnée de 3 points...Équation cartésienne d’un plan
L’équation cartésienne d’un plan est une expression de la forme ax+by+cz+d=0. Pour explorer les propriétés de ce type de représentation, l’outil essentiel est le produit scalaire de 2 vecteurs.
1. Produit scalaire de 2 vecteurs
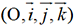 orthonormal. Si
orthonormal. Si 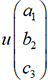 et
et 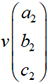 sont deux
vecteurs de l’espace, leur produit scalaire
sont deux
vecteurs de l’espace, leur produit scalaire 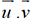 est le nombre a1a2 + b1b2 + c1c2. Les
deux définitions suivantes en résultent :
est le nombre a1a2 + b1b2 + c1c2. Les
deux définitions suivantes en résultent :-
Deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul.
-
Un vecteur est normal à un plan si et seulement s’il est orthogonal à tout vecteur de ce plan (en fait, il faut et il suffit qu’il soit orthogonal à 2 vecteurs non colinéaires du plan).
2. Équation d’un plan défini par un de ses points et par un vecteur normal
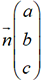 un vecteur normal au plan
(P), avec (a;b;c)≠(0;0;0), et soit A(xA;yA;zA) un point
du plan (P). Si M(x;y;z)
est un point quelconque du plan (P), le produit scalaire
un vecteur normal au plan
(P), avec (a;b;c)≠(0;0;0), et soit A(xA;yA;zA) un point
du plan (P). Si M(x;y;z)
est un point quelconque du plan (P), le produit scalaire 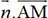 doit être nul puisque
doit être nul puisque 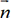 est un vecteur normal du plan.
est un vecteur normal du plan.On a donc a(x-xA)+b(y-yA)+c(z-zA)=0 d’où on tire l’équation cartésienne du plan (P) : ax+bx+cz-(axA+byA+czA)=0.
# Équation cartésienne d'un plan défini par 1 point et 1 vecteur
# normal
from math import*
xA,yA,zA=eval(input("Coordonnées du point A ? "))
a,b,c=eval(input("Coordonnées du vecteur normal au plan... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

