Énoncé 2 : Tableaux
Introduction
Durée
8 heures 50
Mots-clés
tableau, indice, dimension, recherche, tri, fusion
Objectif
Dans ce chapitre, vous apprendrez à :
-
déclarer des tableaux ;
-
créer des tableaux en Java ou en Python ;
-
utiliser les indices pour affecter et lire un élément d’un tableau.
Prérequis
Pour valider les prérequis nécessaires avant d’aborder le TP, répondez aux questions ci-après.
1. Questions générales
|
1. |
Combien une variable de type tableau ayant n éléments contient-elle de valeurs ? |
|
2. |
Combien une variable de type tableau à plusieurs dimensions possède-t-elle précisément de valeurs ? |
2. Questions Java
|
3. |
Quels éléments figurent dans la déclaration d’une variable tableau en Java ? |
|
|
|
a. |
le nom de la variable tableau ; |
|
|
b. |
le type des éléments du tableau ; |
|
|
c. |
la borne inférieure du tableau ; |
|
|
d. |
le nombre d’éléments du tableau ; |
|
|
e. |
le nombre de dimensions du tableau. |
|
4. |
Comment est déclaré le tableau t d’entiers à deux dimensions ? |
|
|
5. |
Quel est l’opérateur qui permet de créer un tableau et de fixer la taille pour chaque dimension ? |
|
|
6. |
Comment est créé un tableau t d’entiers à deux dimensions de tailles respectives 10 et 20 ? |
|
3. Questions Python
|
7. |
Quelle est la particularité des tableaux en Python ? |
|
8. |
Comment déclarer une variable contenant un tableau vide d’entiers ? |
|
9. |
Comment est créé un tableau d’entiers à deux dimensions avec des valeurs spécifiques (par exemple de tailles respectives... |
Énoncé 2.1 : Moyenne des éléments d’un tableau
Durée estimative : 25 minutes
Écrivez l’algorithme qui remplit un tableau de vingt entiers (tableau d’une seule dimension) en lisant au clavier chaque élément, puis en calcule la moyenne.
Écrivez ensuite le programme Java/Python correspondant.
Énoncé 2.2 : Variance et écart type des éléments d’un tableau
Durée estimative : 35 minutes
Complétez l’algorithme précédent en ajoutant le calcul de la variance et de l’écart type.
Soit M la moyenne des éléments du tableau. La variance est la moyenne des différences entre la valeur de chaque élément du tableau et M élevées au carré, selon la formule suivante :
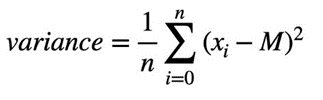
L’écart type est la racine carrée de la variance, soit :
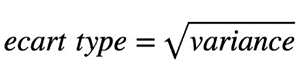
Modifiez ensuite en conséquence le programme Java/Python correspondant.
Indice
En Java, utilisez la fonction Math.sqrt() pour obtenir la racine carrée.
En Python, la fonction sqrt() du paquetage math remplit le même rôle.
Énoncé 2.3 : Recherche séquentielle d’une valeur dans un tableau
Durée estimative : 40 minutes
L’algorithme que vous devez écrire définit un tableau d’éléments de type entier et le remplit avec des valeurs aléatoires comprises entre 1 et 10. Puis il imprime les éléments du tableau. Il lit ensuite une valeur entière et la recherche dans le tableau en commençant par l’indice 0. Chaque fois que la valeur est trouvée dans le tableau, son indice est affiché. Si la valeur entière n’est pas retrouvée dans le tableau, un message est affiché. Dans le cas contraire, le nombre d’occurrences est affiché.
Le calcul du nombre aléatoire n’étant pas demandé dans la partie algorithmique, vous pouvez appeler la fonction prédéfinie nombreAléatoire avec 1 comme premier paramètre et 10 comme second paramètre. Cette fonction se charge de générer un nombre entier aléatoire compris entre 1 et 10 sans en préciser l’algorithme.
Écrivez ensuite le programme Java/Python correspondant.
Améliorez et optimisez enfin l’algorithme et le programme pour que, dès qu’ils trouvent cette valeur entière dans le tableau, ils affichent son indice et s’arrêtent.
Indice
En Java, pour générer...
Énoncé 2.4 : Valeurs communes à deux tableaux
Durée estimative : 55 minutes
Dans un premier temps, l’exercice consiste à écrire l’algorithme qui définit deux tableaux de dix éléments de type entier et qui les remplit avec des valeurs aléatoires comprises entre 1 et 10.
Le contenu de ces deux tableaux est affiché, élément par élément.
Enfin, l’algorithme calcule et affiche le nombre de valeurs communes aux deux tableaux.
Dans une première version de l’algorithme, ne tenez pas compte de la répétition d’une valeur dans le premier tableau.
Dans une seconde version de l’algorithme, respectez la règle suivante : si une même valeur est présente dans les deux tableaux et également présente plusieurs fois dans l’un ou dans les deux tableaux, elle n’est comptée qu’une seule fois.
Écrivez les deux programmes Java/Python correspondants.
Énoncé 2.5 : Insertion d’une valeur dans un ensemble d’entiers
Durée estimative : 25 minutes
Pour représenter un ensemble, deux variables sont nécessaires :
-
un tableau dont la taille représente la taille maximale de l’ensemble ;
-
une variable de type entier dont la valeur est la taille de l’ensemble.
Un ensemble peut contenir une valeur ou non mais il ne peut pas la contenir plus d’une fois (pas de doublon).
Dans cet exercice, nous considérons un ensemble d’entiers dont la taille maximale est de 10. Écrivez l’algorithme qui définit ces deux variables, initialise la taille de l’ensemble à 0 puis lit au clavier des valeurs entières pour les introduire dans l’ensemble jusqu’à ce que la taille maximale de celui-ci soit atteinte. L’algorithme prend soin de ne pas insérer deux fois la même valeur dans l’ensemble. Enfin, l’algorithme affiche le contenu de l’ensemble.
Écrivez ensuite le programme Java/Python correspondant.
Énoncé 2.6 : Suppression d’une valeur dans un ensemble d’entiers
Durée estimative : 25 minutes
Nous considérons à nouveau un ensemble décrit par un tableau et une variable entière contenant sa taille.
Écrivez l’algorithme réalisant la suppression d’une valeur de l’ensemble. Cette valeur est lue au clavier. La valeur initiale de l’ensemble est fournie par une constante (qui, bien sûr, ne contient pas de doublon).
Écrivez ensuite le programme Java/Python correspondant.
Indices
Il ne faut pas oublier que la valeur lue au clavier n’est pas nécessairement présente dans l’ensemble.
La suppression d’une valeur présente provoque un « trou » dans le tableau représentant l’ensemble, il convient donc de décaler les valeurs du tableau vers le bas pour « boucher » ce trou.
La création et l’initialisation d’un tableau s’écrivent comme suit (pour un tableau de dix éléments) en langage algorithmique :
Ensemble : tableau[0..9] d’entiers = {1,2,3,4,5,6,7,8,9,10}
Comme suit en Java :
int[] ensemble = new int[] {1,2,3,4,5,6,7,8,9,10};
Enfin de la façon suivante en Python :
ensemble : List[int] = [1,2,3,4,5,6,7,8,9,10]
Énoncé 2.7 : Insertion d’une valeur dans un ensemble d’entiers (version basée sur un tableau trié de valeurs)
Durée estimative : 55 minutes
Nous décrivons toujours un ensemble par un tableau qui contient ses valeurs et une variable contenant sa taille. Nous ajoutons la contrainte que les éléments du tableau sont triés par ordre croissant.
Écrivez le même algorithme que dans l’énoncé 2.4 en prenant en compte cette contrainte. Pour rechercher si une valeur existe déjà dans un tableau trié, il convient d’utiliser une approche par dichotomie, dont le principe est le suivant :
Soit un tableau trié par ordre croissant de N éléments (indicés de G=0 à D=N-1). Il faut comparer la valeur de l’élément du milieu, c’est-à-dire d’indice M=(G+D)/2. Trois cas se présentent :
-
Si la valeur recherchée est strictement supérieure à la valeur de l’élément du milieu, on considère un nouvel intervalle de G=M+1 à D et on recommence la comparaison avec la valeur de l’élément du milieu du nouvel intervalle.
-
Si la valeur recherchée est strictement inférieure à la valeur de l’élément du milieu, on considère un nouvel intervalle de G à...
Énoncé 2.8 : Suppression d’une valeur dans un ensemble d’entiers (version basée sur un tableau trié de valeurs)
Durée estimative : 30 minutes
Nous considérons toujours un ensemble décrit par un tableau trié par ordre croissant et une variable entière contenant sa taille.
Écrivez l’algorithme réalisant la suppression d’une valeur (lue au clavier) de l’ensemble. Utilisez l’approche par dichotomie comme expliquée à l’exercice précédent. La valeur initiale de l’ensemble est donnée par une constante qui respecte le tri.
Écrivez ensuite le programme Java/Python correspondant.
Énoncé 2.9 : Suppression des doublons dans un tableau
Durée estimative : 30 minutes
Écrivez l’algorithme qui remplit un nouveau tableau à partir des valeurs d’un premier tableau en supprimant les doublons. Cet algorithme calcule également le nombre d’éléments dans le nouveau tableau (ce nombre est contenu dans une variable entière).
Écrivez ensuite le programme Java/Python correspondant en utilisant un tableau de vingt valeurs. La valeur initiale du tableau est fournie par des valeurs aléatoires comprises entre 0 et 10. Le programme doit afficher toutes les valeurs du tableau initial puis celles du tableau résultat.
Énoncé 2.10 : Tri par sélection d’un tableau d’entiers
Durée estimative : 30 minutes
Écrivez l’algorithme qui trie un tableau d’entiers dans l’ordre croissant à l’aide du tri par sélection dont le principe est le suivant :
Soit un tableau de N éléments (indicés de 0 à N-1).
-
Il faut d’abord placer à l’élément d’indice 0 la plus petite valeur présente dans l’ensemble du tableau : l’algorithme recherche l’élément contenant cette plus petite valeur puis échange la valeur de cet élément avec la valeur présente à l’élément d’indice 0.
-
Ensuite, il faut placer à l’élément d’indice 1 la plus petite valeur présente dans les éléments d’indice 1 à N-1 du tableau : l’algorithme recherche l’élément contenant cette plus petite valeur puis échange la valeur de cet élément avec la valeur présente à l’élément d’indice 1.
-
L’algorithme fait de même jusqu’à l’élément d’indice N-2.
Écrivez ensuite le programme Java/Python correspondant en utilisant un tableau de vingt valeurs. La valeur initiale du tableau...
Énoncé 2.11 : Tri bulle d’un tableau d’entiers
Durée estimative : 30 minutes
Écrivez l’algorithme qui trie un tableau d’entiers dans l’ordre croissant à l’aide du tri bulle dont le principe est le suivant :
Soit un tableau de N éléments (indicés de 0 à N-1).
-
L’algorithme teste à l’aide d’une boucle pour un indice i variant de 0 à N-2 si la valeur présente à l’indice i est bien inférieure ou égale à la valeur présente à l’indice i+1. Si oui, le tableau est trié. Si non, l’algorithme échange les valeurs contenues à l’indice i et à l’indice i+1 et continue sa boucle jusqu’à N-2.
-
Cette boucle de test doit être répétée jusqu’à ce qu’il n’y ait plus aucune permutation. Le tableau est alors trié.
Écrivez ensuite le programme Java/Python correspondant en utilisant un tableau de vingt valeurs. La valeur initiale du tableau est fournie par des valeurs aléatoires comprises entre 0 et 100. Le programme doit afficher toutes les valeurs du résultat.
Énoncé 2.12 : Fusion de deux tableaux triés d’entiers
Durée estimative : 45 minutes
Écrivez l’algorithme qui effectue les opérations suivantes :
-
définit deux tableaux t1 et t2 de tailles 10 et 20 ;
-
définit un tableau t3 de taille 30 ;
-
trie les tableaux t1 et t2 (cette partie doit être indiquée dans l’algorithme mais sans être détaillée) ;
-
affiche les tableaux t1 et t2 ;
-
fusionne les tableaux t1 et t2 dans un tableau t3 tel que t3 soit trié ;
-
affiche le tableau t3.
Écrivez ensuite le programme Java/Python correspondant. Ce programme remplit les tableaux t1 et t2 de nombres entiers aléatoires compris entre 0 et 100. Le tri de t1 et de t2 doit être détaillé dans le programme, en utilisant le tri bulle.
Pour fusionner les deux tableaux t1 et t2, il convient de réaliser une boucle qui va parcourir les éléments des deux tableaux. À chaque itération, le programme choisit l’élément le plus petit des deux tableaux t1 et t2 pour l’insérer dans le tableau t3.
Indice
Il ne faut pas oublier le cas où l’un des deux tableaux t1 et t2 a déjà été entièrement parcouru.
Énoncé 2.13 : Comparaison de deux tableaux de caractères
Durée estimative : 20 minutes
Écrivez le programme Java/Python qui compare deux tableaux de caractères constitués exclusivement de lettres minuscules non accentuées. L’ordre de comparaison utilisé est celui du dictionnaire, c’est-à-dire l’ordre alphabétique des mots qui est basé sur l’ordre alphabétique entre deux caractères.
Pour comparer deux mots, on recherche le premier caractère distinct entre eux. Le mot dont le caractère vient avant dans l’ordre alphabétique est le mot qui précède l’autre. S’il n’y a pas de caractère distinct et que l’un des deux mots est plus court, il précède l’autre, sinon les deux mots sont égaux.
En Java, les opérateurs de comparaison entre deux caractères (type char) donnent le même ordre de comparaison pour deux lettres minuscules non accentuées que l’ordre alphabétique.
En Python, les caractères individuels sont simplement des chaînes de caractères (type str) de longueur 1. Il faut donc recourir aux opérateurs de comparaison de chaînes de caractères dont le fonctionnement est également basé sur l’ordre alphabétique.
Indice
Pour déclarer et initialiser...
Énoncé 2.14 : Lecture et écriture de matrices carrées d’entiers
Durée estimative : 20 minutes
Écrivez le programme Java/Python qui lit puis affiche une matrice carrée dont la taille est fixée par une constante.
Énoncé 2.15 : Somme de deux matrices carrées d’entiers
Durée estimative : 25 minutes
Écrivez le programme Java/Python qui lit deux matrices carrées dont les tailles sont fixées par une constante commune, en calcule la somme puis affiche le résultat.
Indice
La somme de deux matrices se fait élément par élément. Si A et B sont les deux matrices dont C est la somme, alors pour toute paire d’indices i et j, Cij=Aij+Bij.
Énoncé 2.16 : Construction d’un index
Durée estimative : 40 minutes
Soit un tableau mots de chaînes de caractères remplies uniquement de caractères minuscules non accentués et dont la longueur est supérieure ou égale à deux. Ce tableau est trié par ordre alphabétique.
Le but du programme de cet exercice est de construire un index sous la forme d’une matrice appelée indexMots (Java) / index_mots (Python), matrice carrée de taille 26 (le nombre de lettres minuscules non accentuées).
Le principe de l’indexation est que chaque valeur de la matrice indicée par le numéro de deux lettres correspond à l’indice dans le tableau mots du premier mot commençant par ces deux lettres. Si un tel mot n’existe pas, la valeur dans la matrice est -1.
Par exemple, l’indice du premier mot dans le tableau mots commençant par ’c’ et ’e’ est donné par indexMots[2][4]. En effet, la lettre ’a’ a pour numéro 0, ’b’ correspond à 1, etc.
Indice
Pour les chaînes de caractères, le plus simple est de les encoder sous forme de tableaux comme à l’exercice 2.12.
En Java, pour convertir un caractère en entier, il faut utiliser le transtypage. Pour obtenir le numéro d’un caractère contenu dans la variable...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



