Arsenal mathématique
Introduction
Cette annexe présente les outils mathématiques fondamentaux nécessaires et prérequis à appréhender les concepts et techniques présentés dans de nombreux chapitres de cet ouvrage, principalement les chapitres Les sciences informatiques, La cryptographie et L’apprentissage machine.
Notions d’algèbre fondamentales
Dans cette section, nous verrons les notions mathématiques les plus basiques : les fonctions, les sommations, et les autres notions fondamentales. Elles servent de socle pour les analyses mathématiques plus poussées dans les applications scientifiques et technologiques présentées dans cet ouvrage.
1. Fonction mathématique
Une fonction est un objet mathématique fondamental qui associe une valeur d’entrée dans un ensemble de départ - que nous appellerons variable - à une valeur de sortie dans un ensemble d’arrivée - que nous appellerons simplement valeur. Voyons les principales notations et concepts qui permettent de définir et de manipuler les fonctions en mathématiques.
a. Notation de base d’une fonction
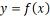
où :
-
f est le nom de la fonction.
-
x est la variable ou argument de la fonction.
-
y est la valeur (de la fonction) pour cet argument x, également notée f(x).
La notation y = f(x) est une façon fondamentale de représenter une fonction en mathématiques. Elle permet de décrire la relation entre la variable x (l’entrée ou argument) de la fonction f et la valeur de sortie y (ou image) produite par cette fonction pour chaque valeur de x. En d’autres termes, y est l’image de x par f, ou y = f(x).
Une fonction exprimée sous cette forme est une règle ou une relation qui associe chaque valeur de x dans un ensemble donné (appelé le domaine de la fonction) à une unique valeur y, souvent dans un autre ensemble (appelé codomaine).
b. Notation ensembliste
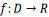
où :
-
D est l’ensemble de départ (ou domaine) de la fonction, c’est-à-dire l’ensemble de toutes les valeurs possibles de x pour lesquelles la fonction f est définie.
-
R est l’ensemble d’arrivée (ou codomaine) de la fonction, soit l’ensemble dans lequel se trouvent toutes les valeurs possibles de f(x).
Introduction à la théorie des ensembles
La théorie des ensembles est une branche fondamentale des mathématiques qui s’intéresse aux collections d’objets ou « éléments ». Ces collections sont appelées ensembles.
La théorie des ensembles est une branche des mathématiques à part entière qui explore des concepts avancés comme les cardinaux infinis, les relations d’ordre, les constructions hiérarchiques d’ensembles infinis, les paradoxes fondamentaux, etc. Mais heureusement nous n’aurons pas besoin de telles notions avancées. Seules des notions fondamentales est assez simples sont nécessaires dans le cadre de cet ouvrage et utilisées par exemple dans le chapitre L’architecture des SI : du mainframe au Big Data du livre L’informatique - Des transistors aux microservices où l’opérateur d’union est nécessaire pour la description formelle de MapReduce à la section Hadoop. Aussi, nous nous bornerons à ne décrire que ces notions essentielles.
1. Opérations fondamentales
Les opérations d’union, d’intersection, de complémentaire, et de différence sont fondamentales en théorie des ensembles. Voyons leur formalisme et les notions sur lesquelles elles s’appuient.
-
Un ensemble...
Introduction au calcul matriciel
Les vecteurs et les matrices sont des concepts centraux en algèbre linéaire, utilisés pour représenter des ensembles de valeurs, des transformations, et des calculs multidimensionnels. Un vecteur est une liste ordonnée de nombres disposée en une seule ligne (vecteur ligne) ou une seule colonne (vecteur colonne), représentant une direction et une magnitude dans un espace donné (en principe depuis l’origine). En pratique, on va interpréter un vecteur comme un point P(x1, x2, ... , xn) dans un espace n-dimensionnel. Une matrice, quant à elle, est une grille de nombres organisés en lignes et en colonnes. Elle permet, par exemple, de manipuler et transformer des ensembles de vecteurs de manière systématique.
Les matrices sont couramment décrites par leur taille. Par exemple, une matrice de taille 3 x 4 a trois lignes et quatre colonnes. Elles peuvent être combinées entre elles et avec des vecteurs via des opérations de calcul matriciel : un ensemble de règles qui permettent de manipuler des matrices, pour les additionner, les multiplier, ou les transposer de manière efficace. Concernant le calcul matriciel, par ailleurs, un vecteur est un cas particulier d’une matrice à une seule colonne. En termes de notations, on utilise en général des majuscules pour désigner des matrices et des minuscules pour désigner des vecteurs. Aussi, le symbole d’un vecteur est en général surligné avec une flèche, mais cette notation est souvent omise.
Voyons les notions et opérations les plus courantes dans le calcul matriciel.
1. Addition de matrices
Deux matrices peuvent être additionnées uniquement si elles sont de même taille. Dans ce cas, l’addition s’effectue en additionnant les éléments correspondants de chaque matrice.
Si nous avons deux matrices A et B de taille 3 x 4 :
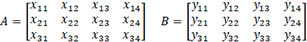
L’addition de A et B, notée A + B, sera une nouvelle matrice C de taille3 x 4 :
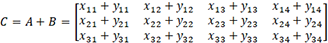
2. Produit scalaire entre vecteurs
Introduction au calcul différentiel
Le calcul différentiel (c’est-à-dire le calcul de dérivées) est fondamental pour un nombre important de sujets dans cet ouvrage. Il se définit comme une branche des mathématiques qui étudie la façon dont les fonctions changent en analysant leurs taux de variation. L’outil central du calcul différentiel est la dérivée.
Les dérivées mesurent la variation d’une fonction et sont indispensables en optimisation et modélisation pour comprendre la pente à un point quelconque de l’espace et donc la direction à suivre pour minimiser ou maximiser le résultat.
1. Calcul des dérivées
 ou encore
ou encore  , est définie comme :
, est définie comme :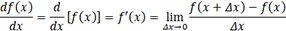
Elle représente en somme la pente de la fonction en tout point, c’est-à-dire le taux de variation de la fonction par rapport à la variable d’entrée. Graphiquement, cela correspond à l’inclinaison de la tangente à la courbe en ce point. Une dérivée positive signifie une fonction croissante, tandis qu’une dérivée négative indique une fonction décroissante.
Voyons les règles de dérivation de base pour les fonctions constantes, linéaires et les monômes. Ces règles forment les fondations des calculs de dérivées pour les fonctions simples.
-
Dérivée d’une constante. Si y = c (où c est une constante), alors la dérivée est zéro, car une constante ne varie pas.
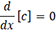
-
Dérivée d’une constante multipliée par une variable. Si
 , alors la dérivée
est simplement la constante c (par
exemple 2 pour y = 2x), car la pente de y = cx est constante.
, alors la dérivée
est simplement la constante c (par
exemple 2 pour y = 2x), car la pente de y = cx est constante.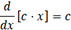
-
Dérivée d’un monôme. Si y = xn (où n est un nombre réel), alors la dérivée suit la règle des puissances, qui consiste à multiplier par l’exposant et à réduire l’exposant de 1.
 Par exemple, pour...
Par exemple, pour...
Introduction à la théorie des nombres
La théorie des nombres est une branche des mathématiques qui s’intéresse aux propriétés et relations des nombres entiers. Dans le contexte de la cryptographie, plusieurs concepts issus de cette théorie sont essentiels pour construire des algorithmes sécurisés. Les notions et théorèmes présentés dans cette section sont nécessaires pour appréhender certains concepts et algorithmes du chapitre La cryptographie.
1. Concepts fondamentaux
Voyons les concepts fondamentaux utilisés en théorie des nombres.
a. Division euclidienne
La division euclidienne est le premier concept fondamental sur lequel sont construites bon nombre d’approches cryptographiques, car elle est utilisée pour calculer le plus grand commun diviseur (PGCD) de deux nombres. C’est un outil central pour résoudre des problèmes d’algèbre modulaire et pour les algorithmes cryptographiques basés sur les clés publiques.
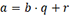
où :
-
 et
et  et
et 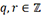
-
et
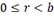
Notations :
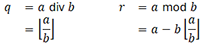
b. Nombre premier
Un nombre premier est un entier supérieur à 1 qui n’a que deux diviseurs : 1 et lui-même.
Les nombres premiers jouent un rôle central en cryptographie, notamment dans les algorithmes comme RSA, où la difficulté de factoriser un grand nombre en produit de deux nombres premiers est une des clés de la sécurité. Les nombres premiers ont plusieurs propriétés qui rendent certaines opérations (comme la factorisation) coûteuses en termes de calcul, assurant ainsi la robustesse de nombreux algorithmes cryptographiques.
Énonçons quelques propriétés :
-
Un nombre p est dit premier si ses seuls diviseurs sont 1 et p.
-
L’ensemble des nombres premiers
 est infini,
est infini, 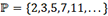
c. Théorème de décomposition
Le théorème de décomposition stipule que tout entier a peut être décomposé de manière unique en un produit de nombres premiers. Précisément, tout entier...
Introduction aux corps finis
Un corps fini (Finite field) est un ensemble particulier d’éléments qui satisfait aux conditions suivantes :
-
Il dispose de la multiplication et de l’addition et ces opérations respectent la commutativité et l’associativité pour tous les éléments.
-
Chaque élément a un inverse pour l’addition.
-
Chaque élément non nul a un inverse pour la multiplication.
Ainsi, on dit qu’un corps est clos par addition et multiplication, et chaque élément a un inverse dans le corps.
Un corps fini est donc un ensemble fini muni des opérations d’addition et de multiplication, satisfaisant les axiomes d’un corps (existence d’un élément neutre pour chaque opération, existence d’inverses, associativité, distributivité, etc.).
 ou GF(q) (Galois Field).
ou GF(q) (Galois Field).Ainsi, un corps fini est aussi appelé un corps de Galois en hommage aux travaux d’Évariste Galois, qui a étudié leur structure et leurs propriétés.
Par exemple :
-
 est un corps fini.
est un corps fini. -
 (les entiers modulo p,
où p est premier)
est un corps fini, car chaque élément non nul
de
(les entiers modulo p,
où p est premier)
est un corps fini, car chaque élément non nul
de  est inversible.
est inversible.
1. Polynômes à coefficients modulaires
 l’ensemble des entiers inversibles
modulo p. On définit
l’ensemble des entiers inversibles
modulo p. On définit  comme l’ensemble des polynômes à coefficients
dans
comme l’ensemble des polynômes à coefficients
dans  . Ces polynômes ont
des coefficients appartenant à
. Ces polynômes ont
des coefficients appartenant à  , et les opérations sur les coefficients
sont effectuées modulo p.
, et les opérations sur les coefficients
sont effectuées modulo p.a. Formalisme
 se décrit
ainsi :
se décrit
ainsi : 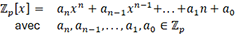
b. Exemple
 :
: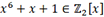
 , c’est-à-dire
des valeurs soit 0, soit 1 (les coefficients sont pris modulo 2).
, c’est-à-dire
des valeurs soit 0, soit 1 (les coefficients sont pris modulo 2). Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations