Les sciences informatiques

Introduction

Les sciences informatiques sont l’étude des principes, des structures et des méthodes permettant de représenter, traiter et transmettre l’information de manière logique et automatisée.

Elles englobent essentiellement l’algorithmique ainsi que l’étude des problèmes informatiques, des algorithmes pour les résoudre et de leur efficacité. L’un des concepts clés dans ce contexte est la complexité algorithmique, qui évalue la vitesse à laquelle un algorithme résout un problème. Les problèmes sont classés par familles de complexité algorithmique comme P (problèmes résolus en temps polynomial) et NP (problèmes vérifiables en temps polynomial). La célèbre question de savoir si P = NP est l’un des grands mystères de l’informatique théorique. Un autre concept clé est la décidabilité, qui désigne la capacité d’un algorithme à déterminer, en un temps fini, si une instance d’un problème donné admet une solution ou non. La théorie de la complexité, domaine à part entière des sciences informatiques, cherche à comprendre et à classer les problèmes selon leur difficulté intrinsèque.

Les sciences informatiques théoriques...

L’algorithmique

Fort de l’arsenal mathématique présenté en annexe et nécessaire à l’appréhension des sujets de ce chapitre, plongeons dans les sciences informatiques, en commençant par l’algorithmique.

L’algorithmique est l’étude des algorithmes et des procédures bien définies permettant de résoudre des problèmes de manière efficace. Un algorithme est une suite finie d’instructions claires qui aboutit à un résultat.

Discipline fondamentale des sciences informatiques, l’algorithmique s’intéresse à la conception, à l’analyse et à l’optimisation des algorithmes pour résoudre des problèmes complexes.

1. Les algorithmes

Les algorithmes existent depuis les débuts de l’informatique, mais leurs racines remontent plus loin. Al-Khwarizmi, mathématicien persan du IX^e siècle, a donné son nom au concept d’algorithme.

Les premières grandes contributions modernes sont venues de figures comme Alan Turing, qui a introduit la machine de Turing en 1936, un modèle abstrait de calcul encore utilisé aujourd’hui pour étudier les limites de la calculabilité.

Un autre pionnier de l’algorithmique moderne, Edsger Dijkstra, a travaillé sur la formalisation des concepts comme la structure des programmes. Dijkstra est célèbre pour ses contributions à l’informatique théorique, notamment avec l’algorithme de Dijkstra pour le plus court chemin dans un graphe (1956) et son travail sur les structures de contrôle des programmes dans les années 60. Il a également introduit des concepts clés tels que l’importance de la preuve de la correction des programmes.

Donald Knuth, avec son œuvre monumentale The Art of Computer Programming, a systématisé l’étude des algorithmes et de leur complexité. The Art of Computer Programming est une série de livres considérée comme une référence incontournable en algorithmique et en structure de données. Publiée pour la première fois en 1968, cette série explore en profondeur les techniques algorithmiques, les méthodes de programmation et l’analyse des algorithmes....

Quelques algorithmes classiques

Voyons quelques algorithmes parmi les plus simples et classiques et évoquons leur complexité.

1. Le tri

Le problème le plus classique en algorithmique est probablement celui du tri (de valeurs dans une liste ou un tableau). De nombreux algorithmes de tri existent, et chacun a ses particularités et ses avantages selon le contexte :

Tri à bulles (Bubble Sort) : un algorithme de tri simple, qui compare des paires d’éléments adjacents du début à la fin de la liste et les échange si nécessaire, répétant le processus jusqu’à ce que la liste soit triée (plus aucun élément à échanger). Il est peu efficace avec une complexité en temps de O(n²) puisque dans le pire des cas (liste triée dans l’ordre inverse à l’ordre cible) il devra répéter les itérations autant de fois qu’il y a d’éléments dans la liste. Le tri à bulles a peu d’intérêt en pratique.
Tri rapide (Quick Sort) : inventé par Tony Hoare en 1960, il utilise la technique de diviser pour régner et est le plus souvent implémenté de façon récursive. La méthode consiste à placer un élément du tableau (appelé pivot, sélectionné plus ou moins aléatoirement,) à sa place définitive, en permutant tous les éléments de telle sorte que tous ceux qui lui sont inférieurs soient à sa gauche et que tous ceux qui lui sont supérieurs soient à sa droite. Cette opération s’appelle le partitionnement et peut être effectuée en O(n). Pour chacun des sous-tableaux, on définit un nouveau pivot et on répète l’opération de partitionnement. Ce processus est répété...

Les structures de données

Les structures de données sont des moyens d’organiser et de stocker des données de manière efficace pour faciliter leur manipulation par des algorithmes. Elles forment certains des outils les plus fondamentaux de la programmation et de l’informatique. Voyons les structures de données les plus communes avec leurs usages, leur histoire, et leurs spécificités.

1. Apparues avec les fondations de l’informatique

L’importance des structures de données est apparue dès les débuts de l’informatique, dans les années 50, lorsque les premiers ordinateurs sont apparus. À cette époque, les scientifiques comme John von Neumann ont compris qu’une structuration efficace des données en mémoire était cruciale pour améliorer les performances des programmes.

L’étude des structures de données s’est ensuite développée dans les années 60 avec l’apparition des langages de programmation, où des structures comme les listes, les tableaux et les arbres sont devenues des outils incontournables pour la gestion des informations.

Les structures de données sont utilisées pour stocker et manipuler des données de manière efficace en fonction des besoins spécifiques des algorithmes. Chaque type de structure de données a ses propres avantages et inconvénients, ce qui les rend adaptées à des problèmes particuliers (et inefficaces pour d’autres). Par exemple, les tableaux sont efficaces pour accéder rapidement à un élément par index, tandis que les listes chaînées permettent des insertions et suppressions efficaces.

2. Les tableaux

Un tableau est une collection de données de même type stockées de manière contiguë en mémoire. Chaque élément est directement accessible par un index. Les éléments peuvent être des valeurs stockées directement dans les cellules mémoire du tableau ou alors des références ou pointeurs vers d’autres structures ou objets plus complexes alloués dynamiquement sur le tas. La plupart des langages fournissent à la fois des mécanismes de bas niveau permettant de créer...

Les paradigmes de résolution

Les paradigmes de résolution en informatique sont des approches algorithmiques générales permettant de résoudre des problèmes de manière systématique. Ces méthodes proviennent de la nécessité de parvenir à trouver des solutions efficaces à des problèmes complexes, souvent issus des mathématiques ou de la logique. Leur utilité réside dans leur capacité à structurer la décomposition de la résolution de problèmes en étapes claires et à exploiter les similitudes présentes dans les données ou les solutions partielles.

Voyons sommairement les plus courants.

1. La récursivité

La récursivité qualifie les situations où une fonction s’appelle elle-même pour résoudre des sous-problèmes plus petits du même problème (on appelle cette approche diviser pour régner ou divide-and-conquer en anglais). Ce mécanisme est inspiré des mathématiques, où des définitions récursives sont utilisées pour exprimer des calculs complexes, comme avec les suites de Fibonacci ou les factorielles. Elle a été théorisée par des pionniers comme Alonzo Church et Alan Turing dans le contexte de la théorie de la calculabilité. En programmation, elle est devenue une approche pratique standard depuis les premiers langages comme LISP et ALGOL, qui en ont fait un principe fondamental.

La récursivité est particulièrement utile lorsque les problèmes peuvent être décomposés en sous-problèmes similaires. Les structures arborescentes (arbres binaires, graphes) et les algorithmes de recherche (parcours en profondeur) sont des exemples typiques d’applications de la récursivité. Un cas d’usage courant est le tri rapide (QuickSort), où l’approche récursive consiste à diviser un tableau en sous-parties plus petites jusqu’à ce qu’elles soient triviales à trier.

Un algorithme récursif repose en général sur deux principes clés :

Cas de base : c’est le cas où le problème est suffisamment simple pour être résolu directement...

L’optimisation mathématique

L’optimisation mathématique et les méthodes associées jouent un rôle central dans de nombreux domaines des sciences informatiques. Les différentes techniques élaborées sont essentielles pour résoudre des problèmes dans des domaines comme la vision par ordinateur, la modélisation statistique, la robotique ou encore l’optimisation de systèmes, où l’objectif est de trouver des solutions optimales ou quasi-optimales dans des systèmes complexes.

La descente de gradient ainsi que des méthodes plus avancées comme celles de Newton et quasi-Newton fournissent des moyens efficaces de minimiser (ou maximiser) des fonctions, qu’il s’agisse de fonctions de coût en apprentissage machine (ML - Machine Learning), de problèmes d’optimisation de réseaux ou de systèmes d’équations différentielles dans la simulation numérique. Ces outils permettent d’itérer vers des solutions optimales en utilisant le calcul différentiel, jouant un rôle fondamental dans un bon nombre d’applications algorithmiques modernes. Par exemple, pour l’apprentissage machine, l’optimisation par descente de gradient est le mécanisme fondamental sur lequel sont construites les techniques d’entraînement. Nous verrons ceci en détail au chapitre L’apprentissage machine.

D’autres problèmes, comme les problèmes d’optimisation de rendement sous contraintes, nécessitent d’autres approches, pour la prise en compte des contraintes ou parce que le problème se formule avec des paramètres discrets. Aussi, l’optimisation mathématique utilisée en algorithmique ne se limite pas seulement à la descente de gradient.

Ces différentes approches sont présentées ci-dessous et dans les sections suivantes. En comprenant ces méthodes, on accède aux fondements théoriques et pratiques de nombreuses applications dans les sciences informatiques, permettant ainsi de résoudre des problèmes complexes avec efficacité et précision. Comme indiqué dans la section Introduction de ce chapitre, cette section et les suivantes assument une bonne compréhension de l’arsenal...

La méthode de Newton

La méthode de Newton est fondamentale en optimisation et en calcul numérique, car elle offre une manière beaucoup plus rapide et efficace, en comparaison avec la descente de gradient « naïve », pour approcher les solutions optimales de fonctions non linéaires.

Elle est ainsi nommée car elle repose sur l’approximation locale d’une fonction pour capturer non seulement la pente locale, comme une approximation linéaire, mais aussi la courbure de la fonction (développement de Taylor d’ordre 2), un concept que Sir Isaac Newton a largement utilisé dans ses travaux sur l’analyse mathématique et le calcul des racines des équations. Bien que Newton n’ait pas explicitement formulé cette méthode sous sa forme moderne, ses recherches sur les solutions d’équations non linéaires ont jeté les bases du principe des approximations successives, qui a ensuite été généralisé en optimisation numérique.

1. Introduction à la méthode de Newton

Pour appréhender la méthode de Newton, il est crucial de comprendre plusieurs concepts mathématiques liés à l’optimisation et à la géométrie des fonctions, notamment la courbure, la convexité, et la distinction entre fonctions convexes et non convexes. Ces notions sont des prérequis pour saisir l’intuition derrière la méthode de Newton et comprendre pourquoi elle peut être plus efficace que la descente de gradient brute dans certains cas. Nous avons déjà parlé de la convexité précédemment, aussi détaillons maintenant la notion de courbure.

a. Relation entre courbure et optimisation

La courbure décrit la manière dont une fonction change de direction lorsqu’on parcourt sa surface (ou courbe, ou hypersurface). Cela est lié à la forme de la fonction et à sa dérivée seconde. Si l’on examine une courbe en deux dimensions :

Courbure positive : si la fonction est concave vers le haut (comme une vallée), sa dérivée seconde est positive.
Courbure négative : si la fonction est concave vers le bas (comme une colline), la...

Autres méthodes d’optimisation

Les techniques d’optimisation mathématique utilisées pour la résolution de problèmes continus ne se limitent pas aux méthodes de descente de gradient ou affiliées comme les méthodes de Newton. Selon la nature du problème à résoudre, des méthodes d’optimisation continue adaptées ou même des méthodes significativement différentes sont utilisées.

1. Autres méthodes d’optimisation continues

Il existe de nombreuses autres méthodes d’optimisation continue, chacune adaptée à différents types de problèmes et d’objectifs. Voyons les principales :

a. La méthode des points intérieurs

Il s’agit d’une technique d’optimisation puissante, souvent utilisée pour résoudre des problèmes d’optimisation convexe avec contraintes. Contrairement aux méthodes traditionnelles de programmation linéaire ou quadratique, qui se déplacent le long des frontières de l’espace des solutions (comme le Simplexe), la méthode des points intérieurs suit un chemin à l’intérieur de la région des solutions admissibles, d’où son nom.

La méthode des points intérieurs s’applique à des problèmes d’optimisation où l’on cherche à minimiser une fonction objectif sous contraintes d’égalité et/ou d’inégalité. Par exemple :

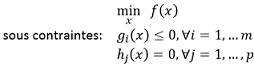
où f(x) est la fonction objectif à minimiser, g_i(x) représente les contraintes d’inégalité et h_j(x) les contraintes d’égalité.

La méthode des points intérieurs repose sur une approche consistant à reformuler le problème des contraintes avec des fonctions de pénalités ou des fonctions de barrière.

Les fonctions de pénalité ajoutent un terme de pénalisation à la fonction objectif, qui devient de plus en plus grand lorsque la solution s’approche d’une contrainte violée. Elles permettent une violation temporaire des contraintes, mais ajustent progressivement le coût pour garantir que la solution finale respecte ces contraintes. Les fonctions...

Les problèmes difficiles

Voyons à présent quelques-uns des principaux problèmes difficiles en algorithmique, les plus classiques, et évoquons leur complexité ainsi que les stratégies pour les résoudre. Nous utiliserons avec un peu d’avance des termes comme NP-difficile, NP-complet ou temps polynomial pour présenter leur difficulté, termes qui seront expliqués dans la section Les classes de complexité. Le lecteur saura s’y référer.

1. La notion de « méthode exacte »

La difficulté des problèmes que nous allons voir s’exprime en considération de la méthode exacte qui qualifie une approche algorithmique garantissant de trouver la solution optimale d’un problème, quelle que soit sa complexité. Contrairement aux heuristiques, la méthode exacte explore en général toutes les possibilités ou utilise des techniques rigoureuses pour s’assurer que la solution trouvée est la meilleure possible.

La solution trouvée par une méthode exacte est toujours la meilleure possible selon le critère fixé (par exemple, minimiser une fonction de coût ou maximiser un bénéfice). Si le problème implique plusieurs solutions possibles, la méthode exacte sélectionne toujours la solution optimale en explorant souvent tout l’espace des solutions possibles :

soit de manière explicite (en testant chaque solution) ;
soit en utilisant des techniques pour explorer les solutions de manière plus efficace mais sans risquer de ne pas trouver l’optimum global.

Des techniques comme la programmation dynamique, la programmation linéaire, ou l’énumération exhaustive sont typiquement utilisées dans le cadre des méthodes exactes.

En raison de leur coût en temps et en ressources, les méthodes exactes sont souvent limitées à des problèmes de petite taille ou à des cas où la garantie d’optimalité est indispensable. Pour des problèmes plus grands, les méthodes heuristiques ou approximatives sont souvent préférées, car elles peuvent fournir des solutions proches de l’optimum beaucoup plus rapidement. Beaucoup de...

Les métaheuristiques

Les métaheuristiques représentent une classe d’algorithmes qui jouent un rôle essentiel en pratique dans la résolution de problèmes complexes, notamment ceux qui impliquent de vastes espaces de recherche et des solutions optimales difficiles à obtenir par les méthodes traditionnelles. Contrairement aux méthodes exactes, qui visent à fournir une solution optimale en explorant systématiquement toutes les possibilités (ou en les éliminant par des techniques avancées), les métaheuristiques adoptent une approche approximative et adaptative. Ces méthodes sont conçues pour trouver des solutions satisfaisantes en un temps raisonnable, souvent en sacrifiant l’optimalité pour privilégier la rapidité et l’efficacité. Elles sont indispensables pour les problèmes où les calculs exacts sont pratiquement inapplicables.

Les méthodes exactes, telles que l’algorithme du simplexe pour la programmation linéaire ou l’algorithme branch-and-bound pour des problèmes combinatoires, visent à trouver une solution optimale prouvée, souvent unique. Mais pour de nombreux problèmes, ces méthodes deviennent rapidement inefficaces ou impraticables à mesure que la complexité augmente. Pour des problèmes de grande taille dans des espaces de recherche combinatoires, les méthodes exactes nécessitent la plupart du temps un temps de calcul exponentiel.

Les métaheuristiques, quant à elles, adoptent des stratégies d’exploration et d’exploitation pour parcourir l’espace des solutions sans l’examiner exhaustivement. Leur flexibilité leur permet de s’adapter à divers types de problèmes d’optimisation difficiles. Mais à nouveau, plutôt que de garantir une solution optimale, elles visent à offrir une solution de qualité en un temps raisonnable, ce qui est souvent indispensable en pratique puisque le temps ou les ressources sont limités.

Les métaheuristiques diffèrent également des méthodes de Newton ou de la descente de gradient utilisées dans l’optimisation continue. Ces dernières, bien qu’efficaces pour les problèmes où...

Les classes de complexité

Les classes de complexité sont des catégories (ou classes) utilisées en informatique pour exprimer la difficulté des problèmes en fonction du temps ou des ressources nécessaires pour les résoudre.

La classe P regroupe les problèmes qui peuvent être résolus en temps polynomial par un algorithme déterministe, c’est-à-dire efficacement.

En revanche, la classe NP contient les problèmes pour lesquels une solution peut être vérifiée en temps polynomial, mais pour lesquels il n’existe pas nécessairement d’algorithme permettant de les résoudre efficacement (c’est-à-dire en temps polynomial).

L’étude des classes de complexité P et NP remonte aux années 1960 et 1970, avec l’essor de la théorie de la complexité computationnelle. Les premières questions sur la distinction entre les problèmes résolus efficacement (P) et ceux dont la solution peut être vérifiée efficacement (NP) remontent aux travaux de chercheurs comme Jack Edmonds, Richard Karp et Stephen Cook. En 1971, Stephen Cook a formalisé la classe NP-complet et a introduit la célèbre question « P = NP ? », qui reste l’un des plus grands défis non résolus en informatique aujourd’hui.

1. La complexité polynomiale

Le terme polynomial en théorie de la complexité informatique fait référence à la façon dont la durée d’exécution d’un algorithme croît en fonction de la taille de son entrée (généralement notée n). Le concept repose sur l’analyse de la manière dont le temps d’exécution d’un algorithme évolue en fonction de cette dernière. Un algorithme fonctionne en temps polynomial si son temps d’exécution peut être exprimé comme une fonction polynomiale de la taille de l’entrée. Autrement dit, l’algorithme est efficace si son temps d’exécution est proportionnel à une puissance de la taille de l’entrée, telle que O(n^k) où k est un entier positif (qui représente le degré du polynôme) et les coefficients...

Du data mining à la data science

L’extraction de connaissances à partir de données n’est pas un concept nouveau. Depuis les débuts de l’informatique, l’exploitation des données est au cœur des applications décisionnelles et scientifiques. Cependant, à partir des années 90, sous l’effet de l’accumulation massive de données issues des bases relationnelles et des entrepôts de données (Data Warehouse), le besoin d’aller au-delà des simples requêtes et agrégations statistiques a mené à l’apparition du Data Mining. Cette discipline, inspirée de la statistique, de l’intelligence artificielle et de l’analyse exploratoire des données, proposait des techniques visant à extraire des régularités, des associations, ou encore à construire des modèles prédictifs à partir de données souvent volumineuses mais encore structurées.

Quelques années plus tard, le contexte change brutalement avec l’avènement du Big Data et la diversité croissante des sources de données : réseaux sociaux, capteurs, logs ou encore données multimédias. Le paradigme et les outils du Data Mining classique ne suffisent plus. C’est dans ce contexte que la Data Science s’impose comme un prolongement naturel mais élargi du Data Mining, intégrant de nouvelles compétences, de nouveaux outils, et des méthodes adaptées à la variété et à la masse des données modernes (les fameux 3V - variété, volume et vélocité - du Big Data).

1. Le data mining

Le Data Mining s’est développé dans les années 1990 suivant l’apparition...

La recherche d’information

La recherche d’information (IR - Information Retrieval) consiste à retrouver, dans un ensemble de documents, ceux qui sont les plus pertinents par rapport à une requête exprimée par l’utilisateur. Si le concept de recherche de documents n’est pas récent (catalogues de bibliothèques, archives), son importance a pris une ampleur considérable avec l’avènement d’Internet et la disponibilité d’immenses volumes de documents numériques, sans structure homogène, souvent bruités et redondants. Le problème fondamental est simple à formuler : comment retrouver efficacement les documents pertinents sans avoir à parcourir l’ensemble de la collection ?

C’est dans ce cadre que sont apparus les premiers systèmes de recherche Internet dans les années 1990, tels que Yahoo!, Altavista puis Google, dont le succès a reposé en partie sur l’efficacité de ses algorithmes d’indexation et de classement. La recherche d’information est ainsi devenue un enjeu central de l’économie numérique.

Au cœur du problème se trouvent deux difficultés : la nécessité de construire des indexes permettant un accès rapide aux documents pertinents, et celle de définir des mesures de pertinence adaptées, capables de déterminer si un document est plus ou moins répondant...

La théorie de l’information

La théorie de l’information est une discipline mathématique qui quantifie l’incertitude, la complexité, et la transmission d’informations dans divers systèmes, de l’informatique aux sciences physiques. Introduite par Claude Shannon en 1948, elle étudie la quantité d’information contenue dans un message ou un ensemble de données et se concentre sur la manière d’encoder, de transmettre, et de préserver cette information de manière optimale, tout en minimisant les erreurs et la perte.

Un concept central de cette théorie est l’entropie, qui mesure l’incertitude associée à une source d’information et fixe des limites théoriques pour la compression et la prédictibilité d’un système. Ce concept est également essentiel pour quantifier la sécurité en cryptographie, l’aléatoire en statistique, ou encore la diversité des données en apprentissage machine.

Au-delà de la communication et du stockage de données, la théorie de l’information offre un cadre universel pour analyser et optimiser les processus d’information dans des domaines aussi variés que les neurosciences, la biologie, et les systèmes intelligents, apportant des outils mathématiques puissants pour interpréter et exploiter les données de manière optimale dans de nombreux contextes.

1. Information et quantité d’information

En théorie de l’information, le terme information désigne une mesure de l’incertitude ou de la réduction d’incertitude dans un système, correspondant à la quantité de nouveauté ou de précision qu’un message, une observation ou un ensemble de données apporte. Elle représente l’ensemble des éléments qui modifient notre connaissance d’un système ou d’un état, en réduisant l’ambiguïté et en augmentant la clarté sur les configurations possibles. Ainsi, au-delà du simple contenu d’un message ou d’un jeu de données, comme nous la concevons en informatique, l’information englobe tout ce qui aide à mieux comprendre...

Et tant d’autres sujets...

Dans ce chapitre, nous avons exploré les fondements des sciences informatiques en évoquant les structures de données, l’optimisation, les problèmes de complexité, etc. Cependant, les sciences informatiques couvrent bien d’autres domaines essentiels qui mériteraient un approfondissement. Un livre entièrement dédié à les présenter ne suffirait pas.

Voici une liste des sujets non abordés les plus essentiels en sciences informatiques, ceux qui jouent un rôle fondamental aussi bien dans la théorie que dans ses applications.

Automates et langages formels : ce domaine se concentre sur la modélisation des langages et des structures syntaxiques par le biais d’automates finis, de grammaires formelles et de machines de Turing, essentiel en compilation et analyse de langages.
Théorie des graphes : utilisée pour modéliser des réseaux et des relations, la théorie des graphes est cruciale pour les algorithmes de parcours, de coloration, et d’optimisation dans les réseaux sociaux, les réseaux de communication et la biologie computationnelle. Nous avons introduit le concept de graphe en parlant des structures de données, mais les sciences relatives à la manipulation de ces structures sont très étendues.
Algorithmes...