La cryptographie

Introduction

La cryptographie est un domaine fondamental des sciences informatiques, au carrefour des mathématiques, de l’ingénierie et de la sécurité. Son rôle principal est d’assurer la confidentialité, l’intégrité et l’authenticité des informations, tant dans les communications numériques que dans la protection des données sensibles. À travers l’histoire, la cryptographie a évolué, passant de techniques simples de chiffrement comme les substitutions, à des algorithmes complexes basés sur des méthodes robustes.

La cryptographie moderne repose largement sur des fondations mathématiques solides, notamment sur la théorie des nombres et l’arithmétique modulaire. Les algorithmes tels que RSA et Diffie-Hellman exploitent ces concepts pour garantir la sécurité, en se basant sur la difficulté de résoudre certains problèmes mathématiques complexes, comme la factorisation du produit de grands nombres premiers ou le calcul du logarithme discret.

La cryptographie a principalement quatre objectifs :

Les principes de cryptographie

1. Histoire de la cryptographie

Avec l’arsenal mathématique nécessaire acquis, abordons maintenant la cryptographie. La cryptographie est une discipline ancienne dont les premières traces remontent à plusieurs milliers d’années. Des civilisations telles que les Égyptiens, les Grecs et les Romains utilisaient déjà des techniques pour chiffrer des messages sensibles afin de préserver la confidentialité des informations échangées.

Un des premiers exemples notables est la scytale, un appareil cryptographique utilisé par les Grecs anciens. Il s’agissait d’un simple bâton autour duquel un ruban de cuir ou de papier était enroulé. Le message était écrit sur le ruban en lignes parallèles, et une fois déroulé, il devenait incompréhensible. Pour lire le message, il suffisait de l’enrouler autour d’un bâton de même diamètre. Ce mécanisme rudimentaire repose sur une clé simple : la dimension du cylindre.

Figure 3-1 - Une scytale (Image dans le domaine public)

Les siècles passant, la cryptographie a évolué pour adopter des approches de plus en plus complexes. Le chiffrement de César, également appelé décalage de César, est une autre méthode historique emblématique. Le procédé consiste à décaler chaque lettre de l’alphabet par un certain nombre de positions. Par exemple, avec un décalage de trois, la lettre ’A’ devient ’D’, la lettre ’B’ devient ’E’, et ainsi de suite. Bien que très facile à casser, cette méthode a été utilisée efficacement par Jules César pour sécuriser ses communications militaires.

Bien sûr...

La cryptographie symétrique

La cryptographie symétrique est l’un des types de cryptographie les plus simples et les plus anciens. Dans cette approche, l’expéditeur et le destinataire partagent la même clé secrète, qu’ils utilisent à la fois pour chiffrer et déchiffrer les messages. La clé est partagée entre les deux parties, et doit donc rester secrète. Toute personne qui découvre cette clé peut déchiffrer le message.

L’objectif principal de la cryptographie symétrique est de garantir la confidentialité de l’information échangée.

Les algorithmes symétriques sont souvent utilisés pour leur vitesse de traitement, en particulier lorsqu’il s’agit de chiffrer de grandes quantités de données. Cependant, le principal défi de ce modèle réside dans la distribution de la clé aux participants. En effet, partager la clé secrète entre les parties de manière sécurisée peut s’avérer compliqué, surtout à grande échelle. Nous verrons plus loin les techniques utilisées à cet effet.

1. Notion de chiffre (cipher)

Un chiffre (ou cipher) est une méthode paramétrée de transformations mathématiques qui prend en entrée un texte clair et une clé pour produire un texte chiffré. Cette transformation est réversible, dans le sens où, avec la bonne clé, il est possible de déchiffrer le texte chiffré et de retrouver le texte clair original.

Formellement, on peut représenter un chiffrement par deux fonctions : une fonction de chiffrement et une fonction de déchiffrement.

a. Fonction de chiffrement

La fonction de chiffrement, souvent notée E, transforme le texte clair x en texte chiffré y, en utilisant une clé secrète k.

Formellement, on écrit :

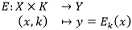
où :

• X est l’espace des textes clairs et x est le texte clair ;

• K est l’espace des clés et k est la clé ;

• Y est l’espace des textes chiffrés et y est le texte chiffré.

L’opération E_k(x) prend un texte clair x et une clé k, et produit un texte chiffré y.

b. Fonction de déchiffrement

De manière...

L’algorithme DES

L’algorithme DES (Data Encryption Standard) est un algorithme de chiffrement symétrique à clé secrète. DES utilise une clé de 56 bits et chiffre des blocs de données de 64 bits à la fois. C’est un chiffrement par blocs (ou tours).

À l’origine de DES est la demande de la création d’un algorithme de chiffrement utilisable par les corporations américaines en mai 1973 par le National Bureau of Standards américain. IBM disposait alors déjà d’un algorithme appelé Lucifer, conçu en 1971 par Horst Feistel. Théoriquement, cet algorithme aurait dû être sélectionné tel quel par le NBS. Ce fut presque le cas mais la NSA demanda qu’une version modifiée par ses soins de Lucifer soit considérée : Cette version fut appelée DES et adoptée comme standard en novembre 1976.

L’algorithme DES fonctionne sur le principe d’un réseau de Feistel, qui implique un découpage du texte en clair en deux moitiés, puis l’application d’un certain nombre de transformations répétées (16 tours dans le cas de DES) pour créer le texte chiffré.

DES devint le premier algorithme de chiffrement symétrique normalisé à l’échelle mondiale. Il marqua le passage à une cryptographie adaptée à l’informatique moderne. Bien qu’aujourd’hui obsolète, il introduisit des concepts fondamentaux, comme la structure de Feistel, qui servirent de base à de nombreux algorithmes ultérieurs.

L’algorithme AES

L’algorithme AES (Advanced Encryption Standard) est un algorithme de chiffrement symétrique adopté comme standard par le National Institute of Standards and Technology (NIST) en 2001. Il a été conçu pour succéder à DES, et offrir un niveau de sécurité élevé pour les données numériques modernes.

AES, également connu sous le nom de Rijndael, a été développé par deux cryptographes belges, Vincent Rijmen et Joan Daemen. Leur algorithme a été choisi après un appel mondial lancé par le NIST, auquel ont participé de nombreuses propositions venant du monde entier. AES s’est distingué par sa sécurité, sa rapidité et sa simplicité d’implémentation sur des plateformes matérielles et logicielles diverses.

AES fonctionne sur des blocs de 128 bits, avec trois tailles de clés possibles :

Les transformations appliquées au cours de chaque tour assurent la sécurité et l’efficacité du chiffrement en combinant des opérations de substitution et de permutation soigneusement conçues.

1. Architecture générale d’AES

Le processus de chiffrement AES peut être divisé en plusieurs étapes :

• Tour initial :

• AddRoundKey : une opération XOR entre l’état (le bloc de texte clair) et la clé de tour.

• Tours principaux (répétés 9, 11 ou 13 fois selon la taille de la clé) :

• SubBytes : une substitution non linéaire appliquée à chaque octet.

• ShiftRows : un décalage circulaire des lignes de la matrice.

• MixColumns : une transformation linéaire appliquée colonne par colonne pour mélanger les octets.

• AddRoundKey : une opération XOR avec la clé de tour.

• Tour final :

• SubBytes

• ShiftRows

• AddRoundKey

Figure 3-7 - Le fonctionnement d’AES

Ce fonctionnement est illustré sur la figure 3-7. Chaque composant de cet algorithme contribue à la sécurité globale en garantissant la confusion et la diffusion dans le texte chiffré final....

Les modes d’opération des chiffres de bloc

Les modes d’opération sont des schémas qui définissent la manière dont les chiffres de bloc (block ciphers) sont utilisés pour chiffrer des messages plus longs que la taille d’un seul bloc. Un chiffre de bloc, comme AES, chiffre les données par blocs de taille fixe (par exemple, 128 bits). Mais dans les applications pratiques, les messages sont souvent bien plus longs que la taille d’un bloc, ce qui nécessite des techniques pour gérer cette longueur supplémentaire. C’est là que les modes d’opération entrent en jeu.

Ces modes d’opération permettent de transformer le chiffrement de blocs de taille fixe en une méthode de chiffrement pour des messages de longueur variable. Ils définissent comment les blocs de texte clair (plaintext) résultant de la découpe du message sont transformés en blocs de texte chiffré (ciphertext) et vice-versa. Il est crucial de choisir le bon mode d’opération car il impacte fortement les propriétés de sécurité du chiffrement, telles que la confidentialité et l’intégrité des données.

Le hachage cryptographique

Le hachage cryptographique (hashing en anglais) est une fonction mathématique qui permet de transformer une donnée d’entrée de taille variable en une sortie de taille fixe, appelée empreinte, image ou haché (hash en anglais). Une fonction de hachage est unidirectionnelle, c’est-à-dire qu’il est très difficile, voire impossible, de retrouver l’entrée d’origine à partir de l’empreinte obtenue. Les propriétés essentielles de ces fonctions sont la résistance aux collisions, la résistance à la préimage, et la résistance à la seconde préimage.

Le hachage cryptographique est une technique clé dans la sécurité de l’information. Les principaux algorithmes de hachage, MD5 et SHA, reposent sur des principes mathématiques solides pour garantir la transformation irréversible des données d’entrée. Les mathématiques derrière les fonctions de hachage sont principalement issues de l’arithmétique modulaire et de l’algèbre booléenne. Par exemple, dans MD5 et SHA, les additions de mots de 32 bits sont effectuées modulo 2³², assurant ainsi que les valeurs restent dans un intervalle fixe. Les transformations comme le XOR ou les rotations circulaires, bien qu’elles soient des opérations réversibles, participent également à l’unidirectionnalité du processus appliquée dans un corps modulaire.

L’histoire du hachage remonte aux années 1950, où les premières fonctions de hachage ont été utilisées pour l’indexation de données dans les bases de données et les systèmes de stockage. Dans les années 1970, avec l’essor de la cryptographie, des fonctions de hachage cryptographiques comme MD4 et MD5 ont été développées pour garantir l’intégrité des données et des communications numériques. En 1993, le gouvernement des États-Unis adopte SHA-1 comme standard de hachage sécurisé, avant que ses faiblesses ne conduisent à l’émergence de la famille SHA-2 (SHA-256, etc.). Aujourd’hui, les fonctions de hachage sont au cœur...

L’authentification

L’un des objectifs les plus cruciaux en cryptographie est d’assurer l’authenticité des informations. Il s’agit de s’assurer que l’information reçue provient bien de l’expéditeur prétendu et n’a pas été modifiée en transit. La cryptographie symétrique, par exemple, permet de garantir cette authenticité en partageant une clé secrète entre l’expéditeur et le récepteur, de manière à ce que les deux parties puissent être assurées de la légitimité du message. Mais l’authenticité ’est pas nécessairement une question de confidentialité, car il doit être possible d’avoir des messages authentiques sans qu’ils soient confidentiels.

Les fonctions de hachage vues précédemment permettent de garantir une certaine forme d’authenticité. Si l’empreinte du message est disponible sur une source sûre, alors elle peut être utilisée pour garantir l’authenticité du message. Mais si une telle source sûre n’existe pas, il faut un moyen plus élaboré pour assurer l’authenticité. C’est là que les Codes d’Authentification de Messages (MAC - Message Authentication Code) entrent en jeu. Mais voyons d’abord le formalisme général.

La cryptographie asymétrique

La cryptographie asymétrique (également appelée cryptographie par clé publique) est un paradigme cryptographique qui permet à deux acteurs (ou plus) de communiquer de manière sécurisée sans avoir à partager une clé secrète au préalable. Contrairement à la cryptographie symétrique, où la même clé est utilisée pour chiffrer et déchiffrer les messages, la cryptographie par clé publique utilise un couple de clés : une clé publique et une clé privée.

Le système repose ainsi sur la génération d’un couple de clés, où ce qui est chiffré avec la clé publique ne peut être déchiffré qu’avec la clé privée correspondante ou vice-versa. Cette asymétrie permet...

Le protocole Diffie-Hellman

Le protocole Diffie-Hellman est l’une des premières méthodes pratiques de cryptographie asymétrique, introduite en 1976 par Whitfield Diffie et Martin Hellman. Son objectif est de permettre à deux parties de convenir d’une clé secrète commune sur un canal public sans jamais partager la clé elle-même directement, clé secrète qui peut ensuite être utilisée pour chiffrer et déchiffrer une communication avec un algorithme symétrique habituel. Ce fut une révolution en cryptographie, car il a ouvert la voie à la sécurisation des communications sans rendre nécessaire un accord préalable sur une clé secrète.

Le protocole Diffie-Hellman a posé les bases de nombreux autres systèmes cryptographiques et a inspiré des concepts fondamentaux tels que les signatures numériques et la cryptographie RSA. Aujourd’hui, Diffie-Hellman est toujours utilisé dans de nombreux protocoles de sécurité, notamment TLS, VPN et d’autres systèmes de communication sécurisée.

L’algorithme RSA

L’algorithme RSA, inventé par Ron Rivest, Adi Shamir et Leonard Adleman en 1978, repose sur le concept des fonctions à sens unique avec trappe (ou trapdoor one-way functions). RSA est largement utilisé pour la cryptographie asymétrique, permettant à deux parties de communiquer en toute sécurité sans même avoir à partager une clé secrète au préalable. La sécurité de RSA repose sur la difficulté de factoriser de grands nombres premiers, un problème qui reste actuellement hors de portée des ordinateurs modernes si les clés sont suffisamment longues (2048 bits ou plus).

Voyons en détail le fonctionnement de RSA.

La cryptographie sur courbes elliptiques

La cryptographie basée sur les courbes elliptiques (ECC - Elliptic Curve Cryptography) est une approche moderne en cryptographie qui repose sur les propriétés mathématiques des courbes elliptiques pour assurer la sécurité des communications. Cette technique a été proposée dans les années 1980 par Neal Koblitz et Victor Miller, qui ont tous deux, indépendamment mais simultanément, travaillé sur ce sujet. Son principal atout est de fournir un niveau de sécurité élevé avec des clés beaucoup plus petites que celles requises par les méthodes classiques comme RSA ou Diffie-Hellman, ce qui en fait une option particulièrement attrayante pour les systèmes embarqués, les appareils mobiles et les environnements où la puissance de calcul et l’espace de stockage sont limités.

1. Principe et fonctionnement des courbes elliptiques

Une courbe elliptique est définie par une équation de la forme suivante (équation de Weierstrass) : où a et b sont des coefficients qui déterminent la forme de la courbe. Dans un contexte cryptographique, la courbe est définie sur un corps fini (avec p un grand nombre premier) ou (en général ) - pour une puissance de nombre premier. En conséquence, les coordonnées x et y ainsi que les coefficients a et b, sont des éléments de ce corps fini (ce qui signifie qu’ils se manipulent modulo p ou pⁿ). Les points de la courbe elliptique sont les paires (x,y) qui satisfont cette équation, en incluant un point spécial appelé le point à l’infini (noté O), qui sert de point neutre pour l’addition sur la courbe.

Les courbes elliptiques possèdent des propriétés géométriques et algébriques...

D’autres algorithmes cryptographiques classiques

Il existe beaucoup d’autres algorithmes ou approches cryptographiques utilisés dans l’industrie. Voyons les plus communs et parlons brièvement de leur fonctionnement et usage.

Les types d’attaques en cryptologie

En cryptographie, plusieurs types d’attaques visent à briser la sécurité d’un algorithme ou à obtenir des informations sur les messages ou les clés. Ces attaques varient en fonction des hypothèses sur les données ou les informations accessibles à l’attaquant. Voyons les principales catégories d’attaques :

La cryptographie et la cryptanalyse quantiques

L’informatique quantique est l’une des révolutions technologiques les plus prometteuses et redoutées du 21^e siècle. Elle tire parti des propriétés uniques de la mécanique quantique, comme la superposition et l’intrication, pour effectuer des calculs d’une manière fondamentalement différente de celle des ordinateurs classiques.

Alors que l’informatique classique repose sur des bits, représentant soit 0 soit 1, un qubit peut exister simultanément dans un état de 0 et de 1 grâce à la superposition, offrant une puissance de calcul exponentiellement supérieure pour certains problèmes. Cette section explore comment ces capacités influencent la cryptographie et la cryptanalyse, transformant des algorithmes essentiels en des outils potentiellement vulnérables.

La sécurité des systèmes informatiques

Parce que c’est très directement lié à la cryptographie, il est opportun dans un tel chapitre de conclure en traitant plus globalement de la sécurité informatique en général.

La sécurité informatique est un domaine essentiel et complexe, centré sur la protection des systèmes d’information et des données contre une large gamme de menaces (threats) et de vulnérabilités. En réponse à la dépendance croissante envers la technologie, l’objectif principal de la sécurité informatique est de préserver la confidentialité, l’intégrité et la disponibilité des informations, souvent abrégées en CIA :